1).Центр тяжести дуги окружности. Рассмотрим дугу AB радиуса R с центральным углом 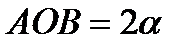 . В силу симметрии центр тяжести этой дуги лежит на оси
. В силу симметрии центр тяжести этой дуги лежит на оси 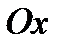 . Найдём координату
. Найдём координату 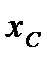 по формулам
по формулам 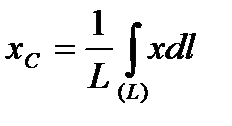 ,
, 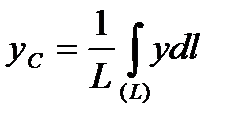 ,
, 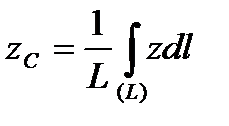 .Для этого выделим на дуге AB элемент
.Для этого выделим на дуге AB элемент 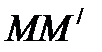 длиною
длиною 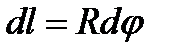 , положение которого определяется углом
, положение которого определяется углом 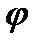 . Координата
. Координата 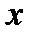 элемента
элемента 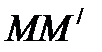 будет
будет 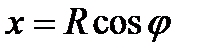 . Подставляя эти значения
. Подставляя эти значения 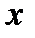 и
и 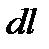 в первую из формул и имея в виду, что интеграл должен быть распространён на всю длину дуги, получим:
в первую из формул и имея в виду, что интеграл должен быть распространён на всю длину дуги, получим: 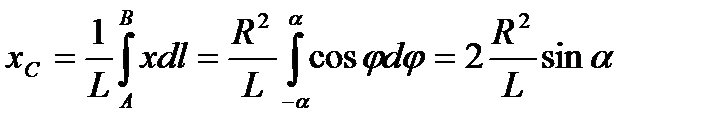 , где L – длина дуги AB, равная
, где L – длина дуги AB, равная 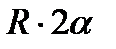 . Отсюда окончательно находим, что центр тяжести дуги окружности лежит на её оси симметрии на расстоянии от центра О, равным
. Отсюда окончательно находим, что центр тяжести дуги окружности лежит на её оси симметрии на расстоянии от центра О, равным 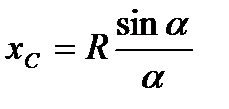 , где угол
, где угол 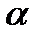 измеряется в радианах. 2). Центр тяжести площади треугольника. Разобьём площадь треугольника ABD прямыми, параллельными стороне AD, на n узких полосок; центры тяжести этих полосок будут, очевидно, лежать в медиане BE треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом известно,
измеряется в радианах. 2). Центр тяжести площади треугольника. Разобьём площадь треугольника ABD прямыми, параллельными стороне AD, на n узких полосок; центры тяжести этих полосок будут, очевидно, лежать в медиане BE треугольника. Следовательно, и центр тяжести всего треугольника лежит на этой медиане. Аналогичный результат получается для двух других медиан. Отсюда заключаем, что центр тяжести площади треугольника лежит в точке пересечения его медиан. При этом известно, 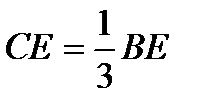 . 3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор OAB радиуса R с центральным углом
. 3) Центр тяжести площади кругового сектора. Рассмотрим круговой сектор OAB радиуса R с центральным углом 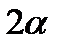 . Разобьём мысленно площадь сектора OAB радиусами, проведёнными из центра О, на n секторов. В пределе, при неограниченном увеличении чиcла n? эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса
. Разобьём мысленно площадь сектора OAB радиусами, проведёнными из центра О, на n секторов. В пределе, при неограниченном увеличении чиcла n? эти секторы можно рассматривать как плоские треугольники, центры тяжести которых лежат на дуге DE радиуса 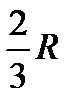 . Следовательно, центр тяжести сектора ОАВ будет совпадать с центром тяжести дуги DE, положение которого найдётся по формуле
. Следовательно, центр тяжести сектора ОАВ будет совпадать с центром тяжести дуги DE, положение которого найдётся по формуле 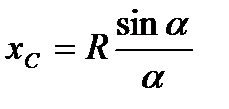 . Окончательно получим, что центр тяжести площади кругового сектора лежит на его оси симметрии на расстоянии от центра О, равным
. Окончательно получим, что центр тяжести площади кругового сектора лежит на его оси симметрии на расстоянии от центра О, равным 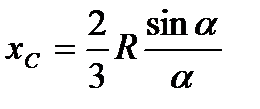 .
.
Центр тяжести дуги окружности, треугольника кругового сегмента.с.135
|
|
Подборка статей по вашей теме:
- Координаты центра тяжести некоторых однородных тел
- Центр тяжести простых геометрических тел
- Центр масс сплошных тел
- Центр тяжести треугольника
- Положения центров тяжести простых геометрических фигур
- Центр тяжести тела
- Сила тяжести и вес
- Пример выполнения расчетно-графической работы по теме «Центр тяжести»
- Центр тяжести кругового сектора
- Правило прямой линии и центра тяжести в тройных системах
- Внецентренное сжатие силой, приложенной на одной из главных осей инерции сечения стержня
 2015-05-30
2015-05-30 1569
1569
