1) для круга;
2) для прямоугольника;
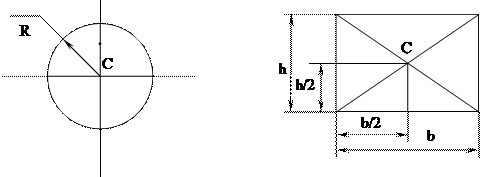
3) Центр тяжести любого треугольника лежит на пересечении медиан.
Частные случаи: для треугольника
- прямоугольного - равнобедренного

4) для полукруга;
5) для четверти круга;
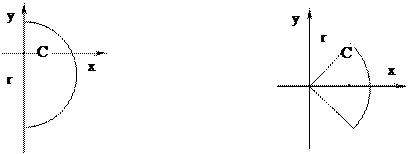
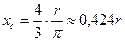
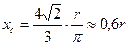
(где r – радиус круга).
Пример 1: Определить положение центра тяжести фигуры, имеющей ось симметрии (размеры определены на схеме).
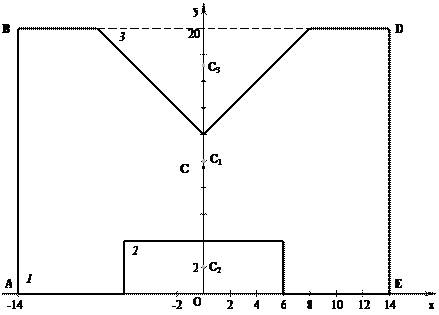
Решение:
Фигура имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось y, а ось x – с нижним основанием фигуры.
Используем метод отрицательных площадей.
1. Разобьем фигуру произвольным образом на простые фигуры.
Наиболее рациональным из всех возможных способов деления фигуры на составные части является тот способ, при котором образуется наименьшее их число.
Дополнив фигуру до прямоугольника ABDE, разобьем ее на три части и определим площадь каждой (в см2):
1 – прямоугольник (большой), 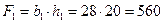 (см2);
(см2);
2 – прямоугольник (маленький), 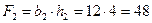 (см2);
(см2);
3 – треугольник, 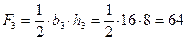 (см2).
(см2).
2. Определяем координаты центров тяжести составных частей:
|
|
|
Точка С1 – ЦТ первой фигуры имеет координаты: 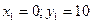 .
.
Точка С2 – ЦТ второй фигуры имеет координаты: 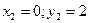 .
.
Точка С3 – ЦТ третьей фигуры имеет координаты:
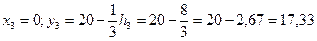 .
.
4. Координаты точки С - центра тяжести всей фигуры:
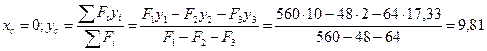 (см).
(см).
Ответ: С (0; 9,81).
Пример 2: Определить положение центра тяжести фигуры, имеющей ось симметрии (размеры определены на схеме).
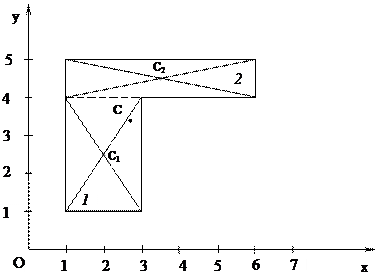
Решение:
1. Разобьем фигуру произвольным образом на простые фигуры (в данном случае на два прямоугольника) определим площадь каждой (в см2):
1 – прямоугольник, 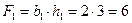 (см2);
(см2);
2 – прямоугольник, 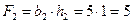 (см2);
(см2);
2. Определяем координаты центров тяжести составных частей:
Точка С1 – ЦТ первой фигуры имеет координаты: 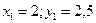 .
.
Точка С2 – ЦТ второй фигуры имеет координаты: 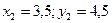 .
.
4. Координаты точки С - центра тяжести всей фигуры:
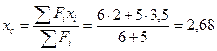 (см)
(см)
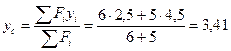 (см).
(см).
Ответ: С (2,68;3,41).
Литература
1. Яблонский А.А., Никифорова В.М. Курс теоретической механики. Ч.1. Статика. Кинематика. М.: Высш. шк., 2004.
2. Куприянов Д.Ф., Метальников Г.Ф. Техническая механика. М., 1995.
3. Цывильский В.Л. Теоретическая механика. М.: Высш. шк., 2004. – 343 с.
 2015-03-22
2015-03-22 17926
17926
