Плотность распределения (ПР), ее свойства

Пусть имеется непрерывная случайная величина 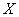с функцией распределения 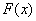, которую мы предположим непрерывной и дифференцируемой.

.

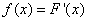Функция 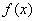- производная функции распределения – характеризует как бы плотность, с которой распределяются значения случайной величины в данной точке. Эта функция называется плотностью распределения (иначе – «плотность вероятности») непрерывной случайной величины .

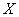Основные свойства плотности распределения.

1. Плотность распределения есть неотрицательная функция:

.

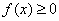Это свойство непосредственно вытекает из того, что функция распределения 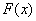есть неубывающая функция.

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

.

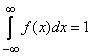Это следует из того, что .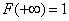

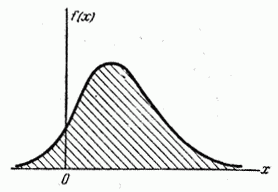
Геометрически основные свойства плотности распределения означают, что:

1) вся кривая распределения лежит не ниже оси абсцисс;

2) полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.