Переходные кривые

В момент въезда автомобиля с прямого участка на кривую в плане скорость движения автомобиля снижают, т.к. на автомобиль начинает действовать центробежная сила. Чтобы в момент поворота колес не происходил занос автомобиля, между прямым участком и кривой малого радиуса вводят так называемую переходную кривую, в пределах которой кривизна дороги плавно изменяется от 0 (на прямом участке) до 1/R в начале круговой кривой.

На автомобильных дорогах I-III категорий радиусы круговых кривых принимают такими, чтобы автомобили проезжали эти участки без снижения скорости. В этом случае длину переходной кривой рассчитывают из условия движения с постоянной скоростью по формуле:

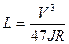, (4.7)

где V - расчетная скорость в км/ч;

J - изменение центробежногоускорения, принимаемое 0,4 - 0,6 м/с³;

R - радиус круговой кривой, м.

Переходная кривая, определяемая по формуле (4.7) называется клотоидой (радиоидою).

Угол поворота клотоиды определяется по формуле

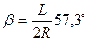(4.8)

и текущие координаты по формулам

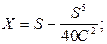
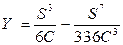, (4.9)

где S – часть длины переходной кривой до данной точки;

С = R·L

При учете движения с переменной скоростью в качестве Рис. 4.2 Расчетная схема переходных кривых проектируют тормозные кривые.

3. Расчет элементов закругления в плане

Последовательность проектирования кривых в плане:

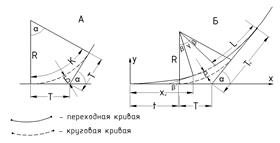
Рис. 4.3 Расчетная схема

1. Определяют элементы закругления:

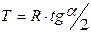; (4.10)

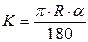; (4.11)

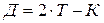; (4.12)

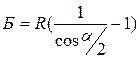, (4.13)

где T – тангенс кривой, м;

К – длина кривой, м;

Д – домер, м.

Б – биссектриса, м.

Вычисления производят с точностью до сотых долей метра.

2. На закруглениях с R ≤ 2000м круговые кривые сопрягают с прямыми при помощи переходных кривых (обеспечивающих плавное изменение центробежной силы), в результате чего круговая кривая смещается к центру, а величина тангенса составной кривой увеличивается (рис.4.3). Длина переходных кривых зависит от радиуса закругления и может быть принята с учетом СНиП 2.05.02-85^*.

Таблица 4.1 – Значения переходной кривой

Радиус круговой кривой, м												600-1000	1000-2000
Наименьшая длина переходной кривой, м

3. Вычисляют длину переходной кривой по формуле (4.7):

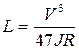4. Вычисляют угол поворота переходной кривой β между касательной к концу переходной кривой, и осью абсцисс.

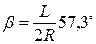(4.14)

и проверяют возможность разбивки переходных кривых, исходя из условия:

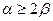. (4.15)

Если это условие не выполняется, необходимо увеличить радиус.

5. Для детальной разбивки определяют конечные координаты переходной кривой по формулам (где С = R·L).

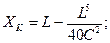
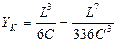, (4.16)

6. Вычисляют величину смещения (t) тангенса

t = X_К – R·sinβ (4.17)

и величину тангенса составной кривой.

T_Н = T+t. (4.18)

7. Определяют длину оставшейся части круговой кривой

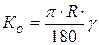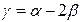; (4.19)

и длину составной кривой

S = K_О + 2L. (4.20)

8. Вычисляют величину сдвижки кривой (р) внутрь

р = Yк – R(1-cos β) (4.21)

и биссектрису составной кривой

Бн = Б + р. (4.22)

9. Вычисляют домер (Д_Н) составной кривой

Дн = 2Тн – S. (4.23)

10. Значения величин t, β и р приведены в табл. 4.2 в зависимости от длины переходной кривой.

Таблица 4.2 – Значения t, β и р

L, м
t, м	19,99	24,95	29,96	34,96	39,97	44,97	49,97	54,98	59,99	50,00
β, º	19º06´	14º19´	11º28´	10º01´	9º10´	8º36´	7º10´	6º18´	3º26´	1º25´58´´
р, м	1,10	1,02	1,00	1,02	1,07	1,12	1,05	1,01	0,60	0,26

Виражи

На кривых малых радиусов для повышения устойчивости автомобилей против заноса устраивают односкатный поперечный профиль с уклоном проезжей части и обочин к центру кривой – вираж. Уклон виража зависит от величины радиуса и скользкости дороги.

Участок, на котором поперечный профиль переходит от двускатного к односкатному, называют отгоном виража. Его совмещают с переходной кривой и, если она отсутствует, то устраивают на прямом участке дороги.

Последовательность изменения поперечного профиля:

1стадия – обочины, как бы вращаются около кромок проезжей части до выравнивания в одну плоскость с уклоном проезжей части (сеч-е 1-1);

2 стадия – наружную половину полотна как бы вращают около оси дороги до выравнивания в одну плоскость с внутренней половиной полотна (сечение 2-2);

3 стадия – все полотно вращают около внутренней

Рис.4.4 Расчетная схема кромки проезжей части до уклона виража (сеч-е 3-3).

Если уклон виража равен уклону проезжей части двускатного профиля (i_в=i_п), то третья стадии отгона виража отсутствует.