Построение и использование графиков при обработке результатов

При выполнении лабораторных исследований часто применяют графический метод обработки результатов измерений. Обязательной частью этого метода является построение графика, который отражает взаимосвязь найденных на опыте численных значений одной физической величины с численными значениями другой величины.

Графики функций строят на миллиметровой бумаге, причём разметка осей координат выбирается удобной по масштабу и состоит из равноотстоящих и не слишком частых меток. Не обязательно, чтобы на осях был отмечен ноль как начало координат: следует использовать именно интервал полученных экспериментальных значений.

Масштаб по осям должен соответствовать погрешностям измерений. Обычно масштабы выбирают таким образом, чтобы полным ошибкам величин, откладываемых по осям, соответствовали отрезки, не меньшие, чем стороны ячейки используемой координатной сетки (т.е. для миллиметровой бумаги 1 мм). При этом масштаб должен быть удобным для использования. Например, при полной ошибке измерения времени равной 0,23с масштаб для оси времени определяется так:

.

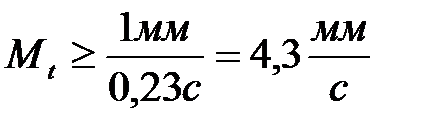В этом случае удобно взять масштаб, при котором 1 секунде соответствует отрезок 5 мм или 10 мм. При этом желательно добиваться того, чтобы экспериментальная кривая располагалась в центральной части графика. На осях указываются обозначения физических величин и единицы их измерений. Для больших или малых значений величин N следует откладывать их по осям без множителя 10ⁿ, а у соответствующей оси сделать обозначение N×10^-n. Дополнительные метки, которые соответствовали бы координатам экспериментальных точек, на осях не выделяют (на осях координат указывают только масштабные единицы). Примеры оформления осей приведены на рисунке 3. Разумеется, аналогичные шкалы строятся и вдоль вертикальных осей. Отмечать на координатных осях значения, соответствующие экспериментальным точкам, не следует.

h, 10-2 м

R, 103 Ом

0,4

0,5

0,6

0,7

t, с

x, мм

Рис. 3

На графике необходимо отмечать сами экспериментальные точки (если кривых несколько – можно для экспериментальных точек использовать разные обозначения: крестики, кружочки, треугольники и т.д., а кривые проводить разными по цвету или виду линиями: штриховыми, штрихпунктирными и т.д.). Точки лучше отмечать карандашом, чтобы можно было легко исправить ошибку, допущенную при построении графика. Когда все экспериментальные точки построены, проводят плавную линию так, чтобы точки наиболее компактно группировались вблизи нее, не обязательно принадлежа ей. График подписывают, определяя построенные зависимости и условия их получения.

При построении графиков недопустимо рисовать изломанную кривую, точно проходящую через все экспериментальные точки: следует провести такую плавную линию, чтобы отклонение экспериментальных точек от нее в разные стороны приблизительно одинаковым.

Для вычерчивания прямолинейных графиков удобно применять прозрачную пластмассовую линейку, а для построения кривых линий – прозрачное лекало. Каждый график сопровождается необходимыми записями: вверху указывается фамилия студента и название работы, к которой относится данный график, по осям указываются масштабы величин Х и Y.

Удобно строить графики в таких координатах, чтобы функция имела линейный характер (эти координаты следует выбирать на основании вида функции y=f(x)). В этом случае график представляет собой прямую линию. Линейная зависимость между величинами Х и Y выражается уравнением вида

Y = аХ + b

где a и b - постоянные (не зависящие от Х и Y) коэффициенты. Довольно часто определение этих постоянных и составляет основную задачу лабораторного исследования.

Существует несколько способов определения величин a и b.

А) Метод натянутой нити

Для построения графика один конец прозрачной линейки закрепляется в точке с координатами (Х ₀, Y₀). Линейку слегка поворачивают так, чтобы экспериментальные точки располагались относительно ее ребра сверху и снизу примерно в одинаковом количестве, и проводят линию. Точки A и В с координатами (X_A, Y_A) и (X_B, Y_B) следует выбирать на прямой линии, поскольку экспериментальные точки имеют естественный разброс вследствие погрешностей прямых измерений X и Y. Среднее значение 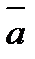по формуле:

Y

X

I

II

III

Рис.4

А

В

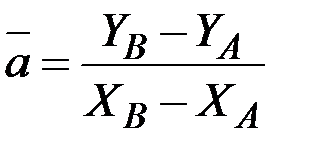. (18)

Для вычисления относительной погрешности 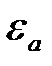с помощью графика поступают следующим образом:

· рабочий участок графика (участок, охватывающий все экспериментальные точки) делят на три равные части (рис.4);

· проводят дополнительную прямую 1 так, чтобы в левой части рабочего участка выше прямой 1 лежало вдвое больше точек, чем под этой прямой, а в правой части – наоборот;

· по формуле, аналогичной (18), вычисляют угловой коэффициент a₁ прямой 1;

· проводят дополнительную прямую 2 так, в левой части ниже прямой 2 находилось вдвое больше экспериментальных точек, чем под этой прямой, а в правой части – наоборот;

· вычисляют угловой коэффициент a₂ прямой 2;

· находят случайную погрешность величины a по формуле

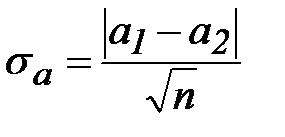, (19)

· где n – количествовсех экспериментальных точек на графике;

· вычисляют относительную систематическую погрешность величины a: ;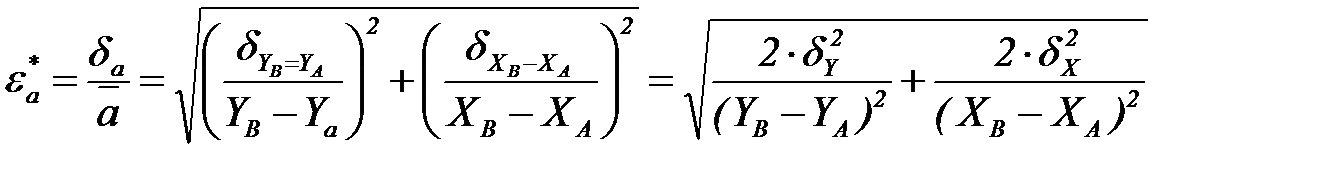

· находят систематическую погрешность величины a:

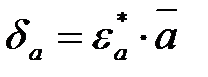; (20)

· зная 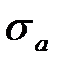и 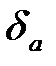, обычным образом вычисляют абсолютную погрешность 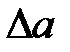, затем – относительную погрешность .

Б) Метод наименьших квадратов

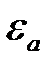Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки. Он также применяется также для приближенного представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке результатов экспериментов.

Когда искомая величина может быть измерена непосредственно, как, например, длина прямой или угол, то, для увеличения точности измерение производится много раз, и за окончательный результат берут среднее арифметическое результатов отдельных измерений. Это правило основывается на соображениях теории вероятности; легко показать, что сумма квадратов отклонений отдельных измерений от среднего арифметического будет меньше, чем сумма квадратов отклонений отдельных измерений от какой бы то ни было другой величины. Само правило представляет, следовательно, простейший случай метода наименьших квадратов.

В этом случае среднее значение 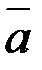вычисляют по формуле по формуле:

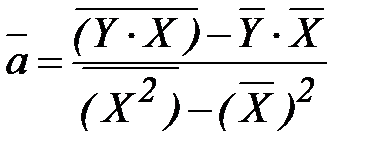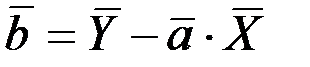, (21)

где , ,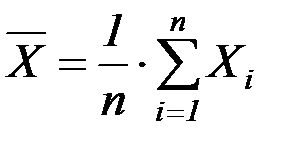

,

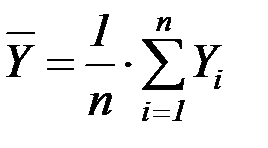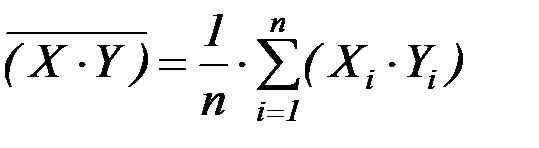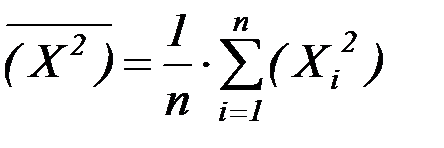
Среднеквадратичные погрешности найденных по формулам (21) параметров оцениваются по формулам

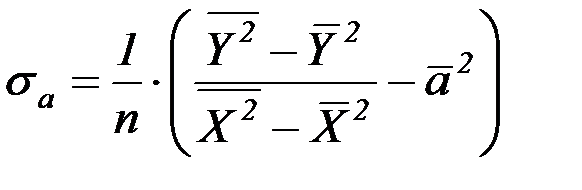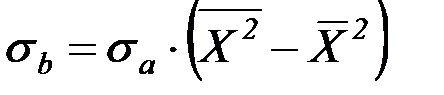, (22)

Однако, вместо формул (21) и (22) можно воспользоваться программой MathCAD на ПК.

При вычислениях косвенно измеряемых величин часто в качестве множителей используются математические и физические табличные данные. В таблицах эти данные записываются только верными цифрами. Цифра приближенного числа называется верной, если абсолютная погрешность числа не превышает одной единицы того разряда, которому принадлежит данная цифра. В противном случае цифра называется сомнительной. Исходя из этого, абсолютную погрешность таких величин принимают равной половине единицы наименьшего разряда. Если взять ускорение свободного падения 9,8 м/с², то абсолютная погрешность величины не превышает 0,05 м/с², а если ее взять равной 9,814, то тогда погрешность будет 0,0005 м/с². Если плотность бензина указана 0,70·10³кг/м³, то абсолютную погрешность можно взять равной 0,005·10³кг/м³.