Случайные погрешности измерений

Если повторять несколько раз измерения одной и той же физической величины (например, массы или, скажем, времени падения груза), стараясь при этом сохранить все условия опыта постоянными, то, тем не менее, полученные результаты будут несколько отличаться друг от друга (конечно, для результатов каждого измерения необходимо записать достаточное количество значащих цифр). Тому существует множество разных причин, которые практически невозможно учесть. Например, неточности в фиксации времени включения и выключения секундомера, которые, кстати, важны для точного определения интервалов времени не только при физических измерениях, но и на спортивных соревнованиях. Как уже указывалось ранее, соответствующие ошибки называют случайными погрешностями.

Со случайными разбросами значений некоторых величин мы встречаемся и в повседневной жизни, например, многократно отмечая время, которое требуется, чтобы доехать до нужного пункта. Случайные величины важны для многих разделов естествознания, например, в молекулярной физике при изучении скорости теплового движения молекул газа или в ядерной физике при изучении закономерностей радиоактивности. Для количественного описания всех таких случайных величин используют хорошо разработанные методы теории вероятностей.

Наиболее вероятное значение любой случайной величины х, а нашем случае результатов нескольких последовательных её измерений (x₁, x₂, x_3…x_n), будем определять как среднее арифметическое значение 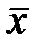по формуле:

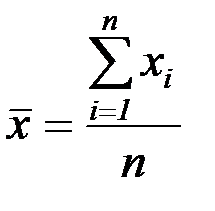, (5)

где n – число измерений.

Несмотря на то, что 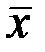является наиболее вероятным значением, оно все же не совпадает с истинным значением а измеряемой величины. Но можно установить интервал значений, за пределы которого с наперед заданной вероятностью ρ не будет выходить значение х. Этот интервал называют доверительным интервалом. А вероятность попадания значений называется доверительной вероятностью или надежностью.

Доверительная вероятность ρ(Δx) в случае непрерывного распределения значений x определяется как:

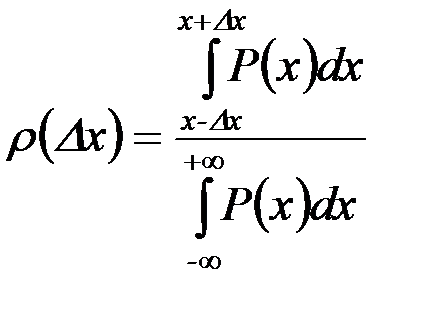, (6)

где P (x) – плотность вероятности реализации значений x в диапазоне от x до x + dx, причем знаменатель в этом выражении обычно принимается равным 1 (условие нормировки).

В теории вероятностей строго обосновывается, что с той же вероятностью ρ(Δx) за пределы этого интервала не будут выходить средние значения x, определенные в различных сериях измерений, в том числе проводимых разными экспериментаторами или на разных, но однотипных установках.

Эти две величины (доверительный интервал и доверительная вероятность) однозначно определяют отличие измеренного значения x от истинного значения физической величины a..

Для определения доверительного интервала помимо 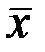необходимо найти среднюю квадратичную ошибку измерений 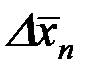в данной серии опытов, которая определяется по следующей формуле:

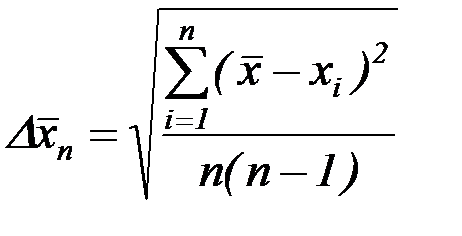. (7)

Вычисление средней квадратичной, а не, как часто делается, средней арифметической ошибки измерений:

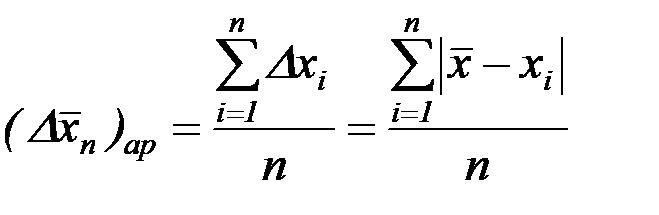, (8)

позволяет более корректно определить затем доверительный интервал.

Путем увеличения числа повторных измерений можно добиться заметного уменьшения случайной ошибки окончательного результата измерений.

Таким образом, при n ®¥, 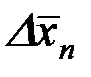®0 и случайную ошибку измерения можно в принципе сделать столь угодно малой величиной, что однако потребует бесконечно долгого процесса измерения.

Определение доверительного интервала для случайной ошибки и, соответственно, отличие среднего значения 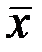от истинного значения этой величины а для заданного значения доверительной вероятности r(Dx) очевидно требует знания конкретного вида функции распределения P_i (x_i) реализации определенных значений x_i.

Рассмотрим вначале наиболее простой для математической обработки, но сложный для практического осуществления случай достаточного большого числа измерений. Строго говоря, для этого необходимо, чтобы n ®¥ и дискретная функция распределения P_i (x_i) переходила в непрерывную функцию плотности вероятности P (x). Однако, как будет показано далее, для этого достаточно n > 100 или даже n > 30. При этом обычно реализуется функция нормального распределения или функция Гаусса, названная так в честь великого немецкого математика, впервые установившего вид этой функции:

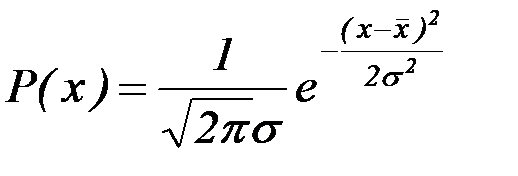. (9)

Здесь использована новая величина s – среднестатистический предел среднеквадратичной ошибки одного измерения при очень большом количестве измерений. Квадрат этой величины s², однозначно определяющей ширину функции распределения для ошибок измерения и вообще распределения случайных величин, называют нормой или дисперсией распределения.

Для обоснования применимости формулы Гаусса необходимо выполнение трех положений, а именно:

— ошибки измерения могут принимать непрерывный ряд значений,

— при достаточно большом числе измерения ошибки одинаковой абсолютной величины, но разного знака, встречаются одинаково часто

— большие ошибки наблюдается реже, чем меньшие.

Тогда измеренные значения величины x, будут находиться внутри доверительного интервала (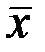 - D x ≤ x ≤ 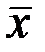+ D x) с доверительной вероятностью r(Dx), определяемой по формуле:

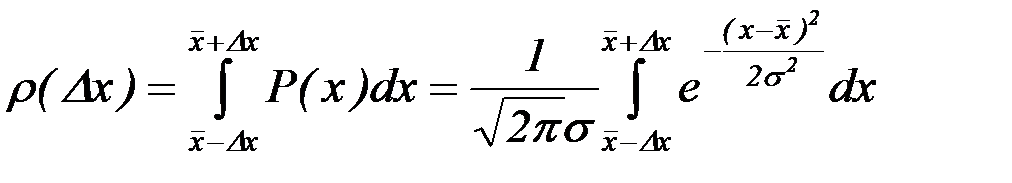. (10)

При этом, чем больше требуется доверительная вероятность r(Dx) и, соответственно, надежность того, что измеренные значения x отличаются от истинного значения этой величины а не более, чем на ±Dx, тем шире по отношению к s становится доверительный интервал. Так, если, например, требуется, чтобы r(Dx) = 0,7; 0,95; 0,98 или 0,999, то соответствующие доверительные интервалы будут равны s; 2s; 2,3s или 3,3s.

Для выбора конкретного значения доверительной вероятности r(Dx), определяющей значения доверительного интервала ±Dx, необходимо понимать, насколько опасен выход за пределы этого интервала, вероятность которого, очевидно, равна 1– r(Dx). Такие задачи возникают на практике, например, при отбраковке изделий, выпускаемых в машиностроительной промышленности, по их габаритам или другим параметрам.

Реально очень трудно осуществить (по причинам большой длительности и малой продуктивности) вышеуказанный идеализированный случай, требующий, чтобы число измерений было, по крайней мере, больше тридцати. Поэтому необходимо рассмотреть реальный, но более сложный для анализа случай относительно небольшого числа измерений (3 < n < 10). Интуитивно понятно, что в этом случае возникают повышенные требования к доверительному интервалу (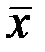 - Dx; 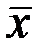+ Dx) при заданном значении r(Dx), то есть он становится шире. Увеличение числа измерений, наоборот, сужает этот интервал.

На опыте часто измеряют физические величины, которые могут принимать лишь дискретные значения, а число этих измерений конечно. В ряде случаев вероятность реализации определенных значений таких величин хорошо описывается распределением Пуассона (знаменитый французский математик и физик).

Для многих лабораторных работ, когда число измерений не велико, распределение погрешностей описывается еще более сложными, специальными гамма–функциями (распределение Стьюдента или “ t ”– распределение. “Стьюдент” – это псевдоним английского математика Уильяма Сита Госсета.). Для такого распределения с высокой точностью вычислены так называемые коэффициенты Стьюдента t, представленные в таблице 1. Они определяют отношение доверительного интервала D x к средней квадратичной ошибке 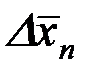для данной серии измерений и определенных значений n и r(Dx), то есть:

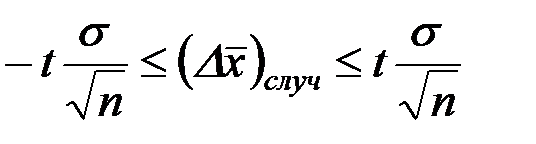(11)

где - так называемая среднеквадратичная или стандартная ошибка отдельного измерения; 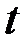- коэффициент Стьюдента.

Среднеквадратичная ошибка определяется на основании результатов повторных измерений путем вычисления по формуле

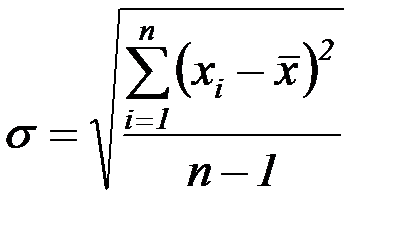(12)

Коэффициент Стьюдента зависит от требуемой, надежности доверительного интервала и от числа измерения. Его значения для 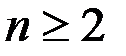и различных 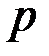вычислены и приводятся в справочниках в виде таблицы (табл. 1). Каждое значение 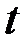располагается в таблице на пересечении строки, соответствующей числу измерений 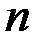, и столбика, соответствующего заданной надежности 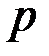. Например, пр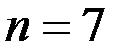и и 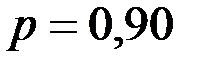(90%) коэффициент Стьюдента имеет значение .

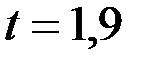Коэффициенты Стьюдента t. Таблица №1.

n (число измер.)	Доверительная вероятность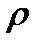
0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	0,95	0,98	0,99	0,999
21-24 26-27	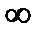0,16 0,14 0,14 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13 0,13	0,33 0,29 0,28 0,27 0,27 0,27 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,26 0,25 0,25 0,25	0,51 0,45 0,42 0,41 0,41 0,40 0,40 0,40 0,40 0,40 0,40 0,40 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39 0,39	0,73 0,62 0,58 0,57 0,56 0,55 0,55 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,54 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,53 0,52	1,00 0,82 0,77 0,74 0,73 0,72 0,71 0,71 0,70 0,70 0,70 0,70 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,69 0,68 0,68 0,68 0,68 0,68 0,68 0,68 0,67	1,38 1,06 0,98 0,94 0,92 0,90 0,90 0,90 0,88 0,88 0,87 0,87 0,87 0,87 0,87 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,86 0,85 0,85 0,85 0,85 0,84	2,0 1,3 1,3 1,2 1,2 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,1 1,0 1,0 1,0	3,1 1,9 1,6 1,5 1,5 1,4 1,4 1,4 1,4 1,4 1,4 1,4 1,4 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3 1,3	6,3 2,9 2,4 2,1 2,0 1,9 1,9 1,9 1,8 1,8 1,8 1,8 1,8 1,8 1,8 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,7 1,6	12,7 4,3 3,2 2,8 2,6 2,4 2,4 2,3 2,3 2,2 2,2 2,2 2,2 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,1 2,0 2,0 2,0 2,0 2,0 2,0 2,0	31,8 7,0 4,5 3,7 3,4 3,1 3,0 2,9 2,8 2,8 2,7 2,7 2,7 2,6 2,6 2,6 2,6 2,6 2,5 2,5 2,5 2,5 2,5 2,5 2,5 2,4 2,4 2,4 2,3	63,7 9,9 5,8 4,6 4,0 3,7 3,5 3,4 3,3 3,2 3,1 3,1 3,0 3,0 2,9 2,9 2,9 2,9 2,9 2,8 2,8 2,8 2,8 2,8 2,8 2,7 2,7 2,6 2,6	636,6 31,6 12,9 8,6 6,9 6,0 5,4 5,0 4,8 4,6 4,5 4,3 4,2 4,1 4,0 4,0 4,0 3,9 3,9 3,8 3,7 3,7 3,7 3,7 3,7 3,6 3,5 3,4 3,3

Из таблицы 1 следует, что при доверительной вероятности r(D x) > 0,7 доверительный интервал D x всегда несколько превышает значение 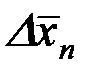, но для r(Dx) = 0,7 по мере увеличения числа измерений n стремится к этому значению, причем их различие становится незначительным (меньше 10%) уже при n ³ 7. Аналогичное, но более медленное уменьшение t наблюдается и для более высоких значений r(Dx) = 0,95; 0,98; 0,999. Для этих значений r, чтобы достаточно приблизиться к предельным значениям t (2; 2,3; 3,3), соответствующим функции Гаусса, необходимо значительно большее число измерений (n > 15, 20 и 40). В большинстве лабораторных работ число измерений (3 < n £ 10), а доверительная вероятность r(Dx) принимается равной 0,95, так что соответствующие коэффициенты Стьюдента изменяются от 4,3 до 2,3. Если значения доверительной вероятности не указаны, то её обычно выбирают равной 0,68 – 0,7.

В практике лабораторных исследований часто указывают лишь среднеквадратичную ошибку , полагая тем самым

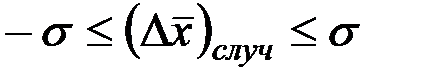(13)

что соответствует теоретическому выводу (11) при условии 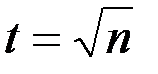. Такому условию, согласно табл.1, при разных 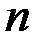отвечают разные значения доверительной вероятности 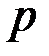. Эти значения приведены в табл.2. Из таблицы видно, что уже при двух повторных измерениях надежность доверительного интервала (14) составляет 61%, а, начиная 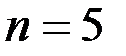,она оказывается выше 90% (более чем в 90 из 100 серий по 5 измерений в каждой среднее значение 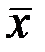обличается от "истинного" не более чем на ).

Для стандартного доверительного интервала зависимость надежности интервала от числа измерений в серии задается таблицей 2.

Таблица 2

Зависимость надежности (доверительной вероятности) стандартного доверительного интервала от числа измерений в серии

Из таблицы видно, что уже при двух повторных измерениях надежность доверительного интервала составляет 61%, а начиная с пяти повторений, она оказывается выше 90%.

Тогда в качестве оценки случайной ошибки s_сл удобно принять среднеквадратичную ошибку, вычисляемую по формуле (6) на основании ограниченного числа измерений n, определяемого по таблице 2.

Полная абсолютная погрешность среднего арифметического 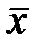оценивается с учетом его и случайной и систематической погрешностей.

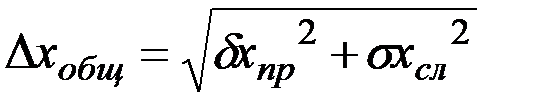(14)

Таким образом, окончательный результат измерений с указанием доверительной вероятности в лабораторных практикумах следует представлять в виде:

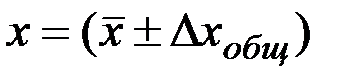, (15)

где за скобкой указывают единицу измерения данной величины, как правило, в общепринятой международной системе единиц (СИ).

При этом необходимо, чтобы среднее значение 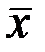и полная абсолютная погрешность D x были записаны в одних и тех же единицах и с одинаковой точностью. Доверительный интервал D x обычно записывают в виде двух (реже одной) значащих цифр, округляя последующие цифры. Если число n измерений совсем невелико (менее 5 – 6), что имеет место в большинстве лабораторных работ, то достаточно округления доверительного интервала до первой значащей цифры, и только если она является единицей – до двух. При большем числе измерений n ~ 10, как правило, следует оставлять одну значащую цифру, если только она больше трёх. При ещё большем числе измерений (n ~ 30 и более) оставляются две значащие цифры. Предварительные вычисления 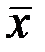и 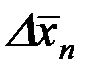следует проводить, разумеется, с несколько более высокой точностью.