Равномощность и мощность множеств

Операции над образами и прообразами отображений и их свойства

Поскольку образы и прообразы отображений являются множествами, то над ними определены все множественные операции: объединение, пересечение, абсолютное и относительное дополнение. Все ранее перечисленные свойства этих операций остаются в силе и для этого случая. Кроме того, имеют место следующие свойства:

Пусть f: A ® B и А ₁, А ₂ Í А и В ₁, В ₂ Í В. Тогда:

1) f (A ₁∪ A ₂) = f (A ₁)∪ f (A ₂).

2) f ^-1(B ₁∪ B ₂) = f ^-1(B ₁)∪ f ^-1(B ₂).

3) f (A ₁∩ A ₂) ⊆ f (A ₁)∩ f (A ₂). Для подтверждения этого свойства рассмотрим А ₁={(x,y): x = y } и A ₂={(x, y): y = x +1} – две параллельные прямые на плоскости. Пусть f: ℝ²® ℝ – проекция на ось х. Тогда f (A ₁) = ℝ и f (A ₂) = ℝ и f (A ₁)∩ f (A ₂) = ℝ; но A ₁∩ A ₂ = Æ и f (A ₁∩ A ₂) =Æ, т.к. проекция пустого множества есть множество пустое, т.о. Æ⊆ℝ.

4) f ^-1(B ₁∩ B ₂) = f ^-1(B ₁) ∩ f ^-1(B ₂).

5) f (A ₁) \ f (A ₂) ⊆ f (A ₁\ A ₂). В подтверждение рассмотрим тот же пример, что и пункте 3. f (A ₁) \ f (A ₂) = ℝ \ ℝ =Æ и A ₁\ A ₂ = A ₁ => f (A ₁\ A ₂) = ℝ. Таким образом, Æ⊆ℝ.

6) f ^-1(B ₁) \ f ^-1(B ₂) = f ^-1(B ₁\ B ₂).

7) Если A ₁⊆ A ₂ => f (A ₁) ⊆ f (A ₂) и если В ₁⊆ В ₂ => f ^-1(B ₁) ⊆ f ^-1(B ₂).

8) (f ^-1◦ f) (A) ⊆ А и (f ◦ f ^–1)(В) = В ∩ f (A).

9) В ∩ f (A)= f (A ∩ f ^–1(В)). Действительно, т.к. В ∩ f (A) = (f ◦ f ^–1)(В), то по свойству композиции (f ◦ f ^‑1)(В)= f (f ^‑1(В)), и т.к. f ^‑1(В) ⊆ А, то f ^‑1(В)= A ∩ f ^‑1(В) => f (f ^‑1(В))= f (A ∩ f ^–1(В))= В ∩ f (A).

Заметим, что если f – взаимно-однозначное отображение, то в пунктах 3, 5 и 8 имеет место равенство.

Два множества А и В называются равномощными или эквивалентными, если между их элементами можно установить взаимно-однозначное соответствие или если существует биекция А на В. Обозначение: А ~ В. Мощность – это то общее, что имеется у всех равномощных между собой множеств. Будем обозначать мощность множества А так: Р(А) или | A |.

Некоторые свойства равномощности:

1) Рефлексивность: А ~ А для любого множества А.

2) Симметричность: для любых множеств А и В, если А ~ В, то В ~ А.

3) Транзитивность: для любых множеств А, В и С, если А ~ В и В ~ С, то А ~ С.

Для доказательства каждого из этих свойств достаточно указать биекцию между множествами. Так в первом случае – это тождественное отображение А на А.

Утверждение: два конечных множества равномощны или эквивалентны тогда и только тогда, когда у них одинаковое число элементов.

Таким образом, мощность характеризует количество элементов множества. И для конечного множества, состоящего из n элементов, его мощность равна n. Для бесконечных множеств понятие «мощности» аналогично понятию «числа элементов», говорят, что бесконечные множества имеют бесконечную мощность. Итак, каждому множеству можно сопоставить некоторый объект – «мощность», называемый также «кардинальным числом», причем | A | = | В | Û А ~ В и | A | < | В | Û $ C Ì B: | A | = | C | и | C | ¹ | B |. Вообще говоря, множество может иметь одинаковую мощность со своим собственным подмножеством.

Примеры:

1) А ={1,2,3,4,5…} и B ={1,4,9,16,25…} Þ А ~ В, т.к. существует биективное отображение А на В по закону f (x)= x ², где x Î А.

2) Функция f (x)=10 x устанавливает равномощность отрезков [0;1] и [0;10].

3) Два любых отрезка [ a, b ] и [ c, d ], а также два любых интервала (a, b) и (c, d) равномощны. Действительно, запишем уравнение прямой, проходящей через точки (а, с) и (b, d): 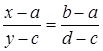. Тогда функция 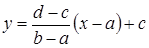, где x Î[ a, b ], взаимно однозначно отображает [ a, b ] в [ c, d ], а функция 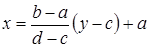, где y Î[ c, d ], отображает [ c, d ] в [ a, b ] и тоже взаимно однозначно.

4) Интервал (-p/2; p/2) ~ ℝ, т.к. y = tg (x), где x Î(-p/2; p/2) – биекция.

5) Любое конечное множество, состоящее из k элементов, равномощно отрезку натурального ряда {1,2,3,¼, k }. Поэтому элементы конечного множества могут быть перенумерованы: а ₁, а ₂,¼, а_k.

Теорема 1.11.1. Конечное множество не равномощно никакому собственному подмножеству и никакому собственному надмножеству.

Теорема 1.11.2. Число элементов конечного множества всегда больше числа элементов любого его собственного подмножества. Или мощность конечного множества всегда больше мощности любого его собственного подмножества.

Теорема 1.11.3. Любое подмножество конечного множества само конечно. Любое надмножество бесконечного множества само бесконечно.

Из последней теоремы следует, что отрезок [0,1] – бесконечное множество, т.к. является надмножеством бесконечного множества чисел вида 1/ n, где n – натуральное.

Бесконечное множество, равномощное множеству всех натуральных чисел называется бесконечно–счетным. Т.е. счетность множества есть не что иное, как возможность перенумеровать все элементы множества при помощи натуральных чисел так, чтобы все числа были использованы и различным элементам соответствовали различные числа. Конечные множества и счетно–бесконечные называются просто счетными.

Свойства счетных множеств.

1) Любое подмножество счетного множества само счетно.

2) Объединение конечного числа счетных множеств – счетное множество.

3) Объединение счетного числа конечных множеств – счетное множество.

4) Объединение счетного числа счетных множеств – счетное множество.

Действительно, обозначим множества М ₁, М ₂,¼, а элементы i –го множества: m_{i 1}, m_{i 2},¼. Существует лишь конечное число элементов m_ik, для которых i + k =2, аналогично существует лишь конечное число элементов m_ik: i + k =3 и т.д.. Перенумеруем сначала все элементы, для которых i + k =2 (например, по возрастающим значениям i), затем (с помощью последующих чисел) все элементы, для которых i + k =3 и т.д.. При этом каждый элемент m_ik получит номер и различные m_ik будут иметь различные номера.

5) Если А и В – счетные множества, то А ´ В – счетное. Действительно, т.к. А ´ В ={(а_i, b_j): a_i Î A, b_j Î B }, то для нумерации таких пар можно воспользоваться той же идеей, т.е. перенумеровать сначала пары, для которых i + j =2, затем с помощью следующих натуральных чисел пары, для которых i + j =3 и т.д..

6) Множество рациональных чисел счетно. Действительно, т.к. ℚ={ x: x = a / b, где a Îℤ и b Îℕ}, то " х ÎℚÞ х является корнем уравнения bx – a =0. Рассмотрим h = b +| a |, перенумеруем сначала все рациональные корни, для которых h =1, затем новые корни, получающиеся при h =2 и т.д..

7) Множество полиномов с рациональными коэффициентами счетно. Сопоставим каждому полиному последовательность (а ₁, а ₂, ¼, а_n), составленную из его коэффициентов. Далее поступим аналогично тому, как это было сделано в пункте 6.

8) Множество всех алгебраических чисел (корней полиномов с рациональными коэффициентами) счетно.

Множество называется множеством мощности континуум, если оно равномощно множеству точек отрезка [0,1].

Теорема 1.11.4. (Кантора) Множество точек отрезка [0,1] несчетно.

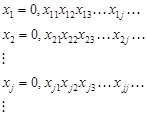Доказательство: (от обратного) пусть это множество счетно. Это означает, что все точки отрезка можно перенумеровать: х ₁, х ₂, х ₃, ¼, х_j, ¼. Каждое число x_j из этого промежутка можно представить в виде бесконечной десятичной дроби с периодом, не равным 9, причем единственным образом. Т.е. x_j = 0, x_{j 1} x_{j 2}¼ x_jj ¼, где x_jk – это k‑ ая цифра десятичной дроби, представляющей число x_j. Построим теперь число b =0, b ₁ b ₂ b ₃¼ b_j ¼ таким образом, чтобы цифра b ₁¹ х ₁₁, b ₂¹ х ₂₂, b ₃¹ х ₃₃, ¼, b_j ¹ х_jj, ¼. Очевидно, это можно сделать, например, взяв каждое b_i =1, если x_ii ¹1, и b_i =2, если x_ii =1. Понятно, что число b Î[0,1], более точно b Î[0.1; 0.3]. Поэтому оно находится среди чисел х ₁, х ₂, х ₃, ¼, х_j, ¼., занимая в этой последовательности некоторое определенное, например, k-ое место. Т.е. b = x_k и 0, b ₁ b ₂ b ₃¼ b_k ¼=0, x_{k 1} x_{k 2} x_{k 3}¼ x_kk ¼. Но тогда b ₁= x_{k 1}, b ₂= x_{k 2}, b ₃= x_{k 3}, ¼, b_k = x_kk, ¼, что невозможно, т.к. выбор b_j осуществлялся так, чтобы b_j ¹ х_jj. Полученное противоречие доказывает теорему.

Из этой теоремы следует, что всякий отрезок [ a, b ] числовой прямой имеет мощность континуум, поскольку [ a, b ]~[0,1], т.к. f (x)= a +(b – a) x, где х Î[0,1] – биекция. Кроме того, всякий интервал (a, b) имеет мощность континуум, поскольку (a, b)~(0,1), а (0,1)~[0,1]; в последнем случае закон биективного отображения может быть, например, таким:

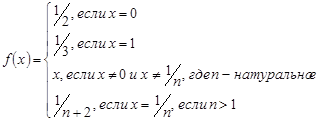
Отсюда также следует, что множество всех вещественных чисел имеет мощность континуум. А также множество всех иррациональных чисел (и иррациональных чисел, содержащихся в любом интервале числовой прямой) несчетно, т.к. оно получается из несчетного множества удалением из него счетного подмножества. Поэтому между любыми двумя вещественными числами найдется иррациональное число и даже несчетно много их.

Из всех бесконечных множеств счетные множества являются «наименьшими».

Теорема 1.11.5. Всякое бесконечное множество содержит счетное подмножество.

Доказательство: (по индукции) Пусть М – бесконечное множество. Тогда М ¹Æ. Выберем какой-нибудь элемент из М и обозначим его а ₁. Пусть в М выбрано уже таким образом n различных элементов: а ₁, а ₂, ¼, а_n. Так как M – бесконечно, то множество A_n = M \ { а ₁, а ₂, ¼, а_n }¹Æ, и можно выбрать элемент из A_n и обозначить его а_{n +1}. Ясно, что а_{n +1} отличается от всех ранее выбранных, и множество { а ₁, а ₂, ¼, а_n }∪{ а_{n +1}} счетно и является подмножеством М.

Теорема 1.11.6. (О равномощности бесконечного множества собственному подмножеству) Всякое бесконечное множество равномощно своему некоторому собственному подмножеству.

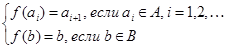Доказательство: по предыдущей теореме множество М содержит счетное подмножество A ={ а ₁, а ₂,¼, а_n, ¼}. Пусть В = М \ А Ê Æ. Определим отображение f: M ® M следующим образом:

Очевидно, что f является биективным отображением множества М на его собственное подмножество М \ { a ₁}, что и доказывает теорему.