2015-05-22
907
1. Пересечением (или произведением) множеств А и В называется множество С, состоящее из всех элементов, принадлежащих одновременно и А, и В:
.
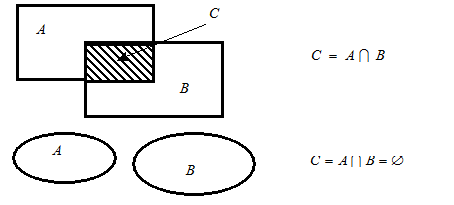
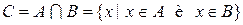2. ОБЪЕДИНЕНИЕМ (или суммой) множеств А и В называется множество С всех элементов, входящих либо в А, либо в В. Причем общие элементы учитываются только один раз: или
.
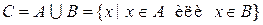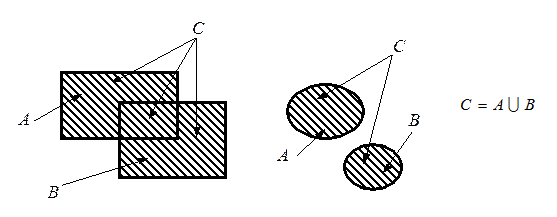
Совокупность – «или»
Система – «и»
3. Разностью множеств А и В называется множество С, состоящее из тех элементов множества А, которые не содержатся в множестве В:
и
.
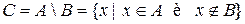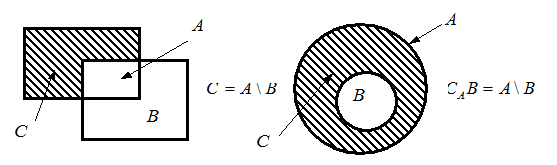
4. Симметрической разностью множеств А и В называется множество С, состоящее из элементов, принадлежащих только А и только В:
.
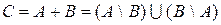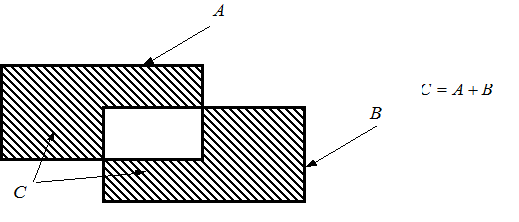
5. Д ополнением множества А называется множество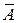 
всех элементов, которые не принадлежат множеству А. Например, если А ={ x| x 
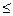2}, то 
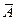={ x| x > 2}.
Введенные выше операции легко распространяются и на несколько множеств. С помощью диаграмм Эйлера можно легко доказать ряд свойств операций с множествами, во многом похожих на обычные арифметические операции. Наиболее часто встречающимися являются следующие свойства:
1. 
; 
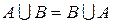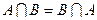– коммутативность.
2. 
; 
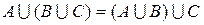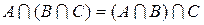– ассоциативность.
3. 
; 
–
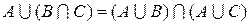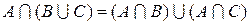дистрибутивность.
4. 
.
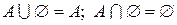5. 
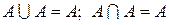– идемпотентность.
6. 
; 
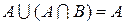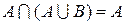– поглощение.
7. 
.
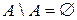8. 
.
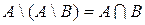9. 
; 
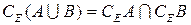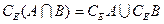– двойственность.
