Соответствие, отображение и функция

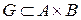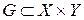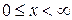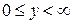Соответствием между множествами A и B называется подмножество . Например, если X – множество всех действительных чисел x от 0 до бесконечности, а Y – аналогичное множество y, то есть первая четверть прямоугольной системы координат, т.е. и . Множество X назовем областью определения соответствия, множество Y – областью значений соответствия.

Под отображением f множества A в множество B (т.е. 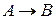) понимается правило, по которому каждому элементу 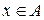сопоставляется единственный элемент 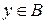. Это отношение обозначим 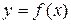. Здесь x называется прообразом элемента y, а 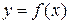называется образом элемента x.

Отображение является обобщением понятия функции. Пусть f определяется выражением: 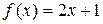. Тогда множеству A действительных чисел X сопоставляется его образ B по данному закону f (x). Другой пример: множеству административных единиц России (x) сопоставляется множество губернаторов f (x), т.е. f (x) = x.

Если имеются три множества A, B, C и известны отображение f для 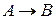и

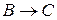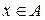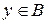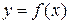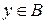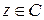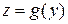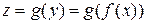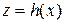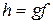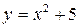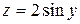отображение g для , то каждому элементу можно сопоставить элемент , т.е. . Так же элементу сопоставляется элемент , т.е. . Обобщая, имеем , т.е. , где – отображение множества A в множество C, называемое композицией (или суперпозицией) заданных отображений. Например, если , а , то 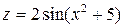. Композиция отображений часто называется сложной функцией.

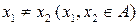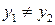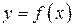Отображение f называют обратимым, если разным прообразам соответствуют разные образы , где и 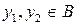. Так как в этом случае единственному образу y соответствует единственный прообраз x, то можно определить обратное отображение 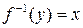. Обратное отображение 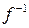устанавливает взаимно однозначное соответствие между множествами A и B. Так для отображения 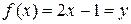легко получить .

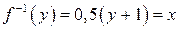Обратное отображение 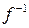часто называется обратной функцией.