Пару элементов a и b называют упорядоченной (или кортежем), если указан первый элемент в этой паре. Пусть a – первый элемент, тогда упорядоченная пара: (a, b). Пары (a, b) и (b, a) считаются различными: 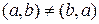 .
.
Аналогично определяются упорядоченные n- ки элементов (при n > 2). Так, упорядоченная пятерка: 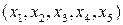 .
.
Прямым (или декартовым) произведением множеств A и B называют множество всех упорядоченных пар (a, b), где 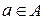 и
и 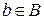 . Обозначение:
. Обозначение: 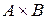 . Пусть, к примеру,
. Пусть, к примеру, 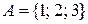 ;
;  . Тогда:
. Тогда:
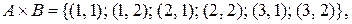
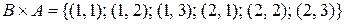
и ясно, что 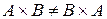 . Иллюстрируем:
. Иллюстрируем:
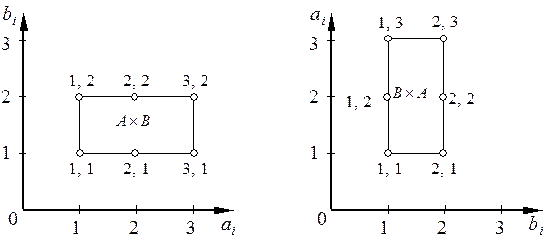
В случае, если 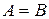 , то удобно обозначать
, то удобно обозначать 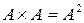 . Если в качестве A принять множество всех точек плоскости, т.е. множество R, то координаты любой точки
. Если в качестве A принять множество всех точек плоскости, т.е. множество R, то координаты любой точки 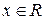 и
и 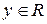 принадлежат множеству
принадлежат множеству 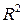 , т.е. декартова система координат является исторически первым примером прямого произведения.
, т.е. декартова система координат является исторически первым примером прямого произведения.
Сформулируем основные свойства прямого произведения для некоторых множеств A, B и C:
1. 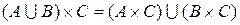 .
.
2. 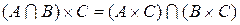 .
.
3. 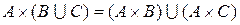 .
.
4. 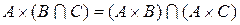 .
.
5. 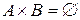 только при
только при 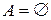 или
или 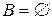 .
.
 2015-05-22
2015-05-22 369
369








