2015-05-22
1247
Задача 1. Даны множества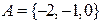 
и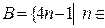 
N}. Какова мощность множеств 
?
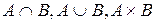Решение. Множество A конечно и задано перечислением своих элементов, множество B задано характеристическим свойством. Запишем несколько первых элементов множества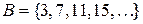 
. Видим, что 
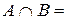Æ и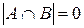 
, т.е. множество 
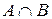конечно.
Покажем, что множество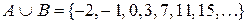 
счетно. Занумеруем его элементы:
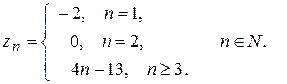
Задана биекция множества N на множество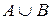 
, следовательно, 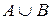счетно и 
.
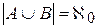По определению декартова произведения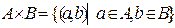 
. Запишем элементы этого множества в виде матрицы (рис. 7) и занумеруем их по столбцам.
|
Замечаем, что если номер n делится на 3 без остатка, то первый элемент пары равен 0; если номер n делится на 3 с остатком 1, то первый элемент пары равен –2; если номер n делится на 3 с остатком 2, то первый элемент пары равен –1. Поэтому способ нумерации может быть задан следующим образом:
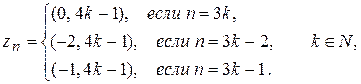
и множество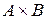 
счетно, т.е. имеет мощность À0.
Задача 2. Равномощны ли множества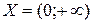 
и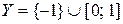 
?
Решение. Покажем, что множества равномощны по теореме Кантора–Бернштейна, т.е. покажем, что найдется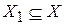 
такое, что 
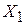равномощно Y, и найдется 
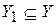такое, что 
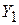равномощно X.
Выберем в качестве 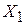множество 
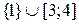и установим биекцию 
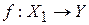следующим образом:
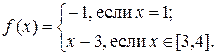
Множества 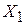и Y равномощны.
Пусть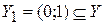 
. Установим биекцию 
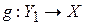по закону 
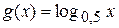. Множества 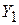и X равномощны. По теореме Кантора–Бернштейна 
.
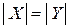Контрольные вопросы и упражнения
1. Является ли биекцией отображение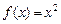 
, заданное на отрезке
[–1;1]? А заданное на [0;1]?
2. Являются ли равномощными множества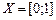 
и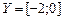 
?
3. Являются ли равномощными множество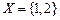 
и множество корней квадратного уравнения 
?
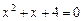4. Сформулируйте теорему Кантора–Бернштейна.
5. Покажите, пользуясь теоремой Кантора–Бернштейна, что множества 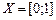и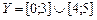 
равномощны.
6. Даны множества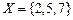 
и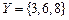 
. Чему равно 
?
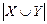7. Впишите ответ: если ,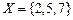 
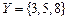, то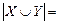 
________.
8. Пусть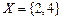 
. Тогда ½B(X)½=______, B(X) = {______________}.
9. Сколько подмножеств имеет множество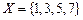 
?
10. Какое множество называется счетным?
11. Покажите, что множество целых чисел Z счетно.
12. Мощность счетного множества обозначается _____.
13. Сформулируйте свойства счетных множеств.
14. Сформулируйте обобщенное правило включения-исключения для трех (четырех) множеств.
