Множество X называется конечным, если существует биекция 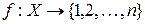 , т.е. множество X можно взаимно однозначно отобразить на отрезок натурального ряда {1, 2, …, n }; при этом ½ X ½= n.
, т.е. множество X можно взаимно однозначно отобразить на отрезок натурального ряда {1, 2, …, n }; при этом ½ X ½= n.
Все множества, для которых такую биекцию установить невозможно, будем называть бесконечными.
Пустое множество принято относить к конечным множествам и обозначать ½Æ½=0.
Сформулируем свойства конечных множеств в виде теорем.
Теорема 1 (правило суммы). Пусть множество X является объединением r непересекающихся конечных множеств 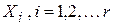 . Тогда
. Тогда 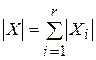 .
.
Согласно условию теоремы система множеств 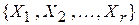 является разбиением множества X.
является разбиением множества X.
Теорема 2 (правило произведения). Пусть конечное множество X представлено в виде декартова произведения r конечных множеств 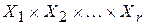 . Тогда
. Тогда 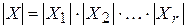 .
.
Теорема 3 (о мощности булеана конечного множества). Пусть множество X конечно и 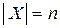 . Тогда
. Тогда 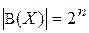 .
.
Напомним, что B (X) есть булеан множества X, т.е. множество всех подмножеств множества X.
Теорема 4 (правило включения – исключения). Пусть 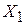 и
и 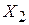 конечные множества. Тогда
конечные множества. Тогда 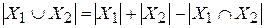 .
.
Теорема 5 (обобщенное правило включения – исключения). Пусть конечное множество X является объединением r конечных множеств: 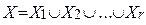 . Тогда
. Тогда
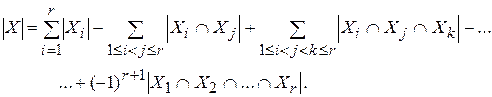
 2015-05-22
2015-05-22 1681
1681
