Кортежи. Декартово произведение множеств

Итак, пусть даны множества 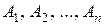. Выберем из первого множества элемент 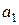, из второго - 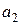и т.д., из множества 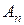выберем элемент 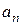. Расположим элементы в порядке их извлечения. Получим упорядоченную последовательность .

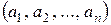Упорядоченная последовательность 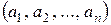, составленная из элементов множеств 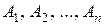, где 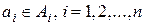, называется кортежем длины п.

Заметим, что множества 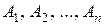могут иметь общие элементы или даже совпадать. Поэтому (в отличие от обычного множества) элементы в кортеже могут повторяться.

Элементы 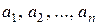кортежа 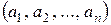называются его компонентами или координатами.

Два кортежа, составленные из элементов одного и того же множества А считаются равными, если их длины равны и элементы, стоящие на соответствующих местах, равны, т.е. = , .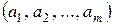

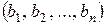
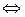
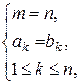
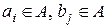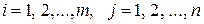Например, кортеж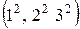и и 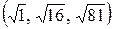равны, поскольку 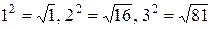, тогда как кортежи 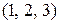и 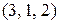различны, хотя имеют одинаковую длину и одно и тоже множество координат, но эти координаты стоят в разном порядке. Различны и кортеж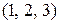и и 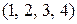- они имеют разную длину.

Координатами кортежа могут быть множества, кортежи и т.д. При этом, например, кортеж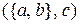и и 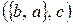равны, так как 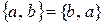, а кортеж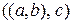и и 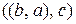различны, так как 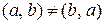. (Поясним 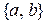- множество, 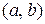- кортеж).

Кортеж, не содержащий ни одной координаты (т.е. кортеж длины 0), называется пустым.

Подчеркнем еще раз отличия понятий кортежа и множества:

а) в множестве порядок элементов не играет роли, а кортежи, отличающиеся порядком элементов, различны даже в случае, если они имеют одинаковый состав;

б) в множестве все элементы различны, а в кортеже координаты могут повторяться.

Чтобы различать множества и кортежи, элементы множеств заключают в фигурные скобки, а элементы кортежей – в круглые (в частности, в круглые скобки заключают элементы упорядоченных множеств).

Введем теперь понятие декартова произведения множеств.

Пусть 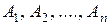- некоторые множества. Их декартовым произведением называют множество, состоящее из всех кортежей вида 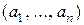, где 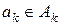, 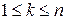. Декартово произведение множеств 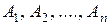обозначают .

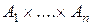Например, если 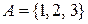, , 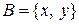то

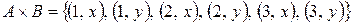и

.

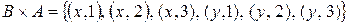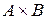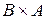Этот пример показывает, что, вообще говоря, декартовы произведения и различны, хотя они содержат поровну элементов.

Различны и множества 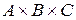, 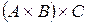и 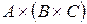- первое состоит из троек 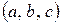, второе – из пар вида 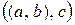, а третье – из пар вида 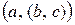, где во всех случаях , , .

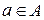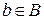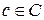Если хотя бы одно из множеств А, В пусто, то считают, что их декартово произведение пусто:

.

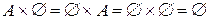Например, декартово произведение 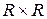состоит из пар 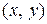действительных чисел, причем 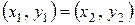в том и только в том случае, когда 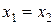, 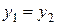. Каждой такой паре соответствует точка 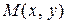на плоскости, для которой числа 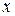и 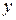являются декартовыми координатами (отсюда название «декартово произведение»). Декартово произведение 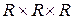состоит из троек чисел 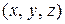, которые можно рассматривать как координаты точки 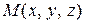в трехмерном пространстве. Декартово произведение 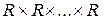(п множителей) называют п-мерным арифметическим пространством. Его обозначают .

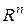Пусть А – произвольное множество и п – натуральное число. Декартовой п-ой степенью множества А называется множество, обозначаемое через 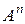и состоящее из всевозможных кортежей длины п элементов из А: .

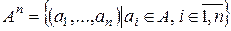В заключение перечислим основные свойства операций над множествами, обозначая буквами А, В, С произвольные множества.

1) 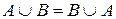(коммутативность операции );

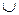2) 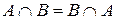(коммутативность операций );

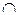3) 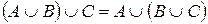(ассоциативность операции );

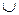4) 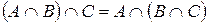(ассоциативность операции );

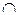5) 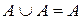(идемпотентность операции );

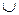6) 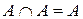(идемпотентность операции );

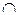7) ;

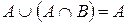8) ;

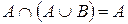9) ;

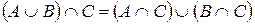10) ;

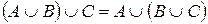11) ;

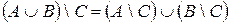12) ;

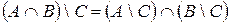13) ;

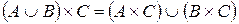14) ;

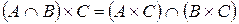15) ;

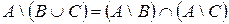16) ;

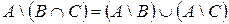17) ;

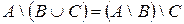18) ;

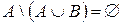19) ;

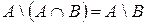20) ;

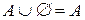21) .

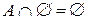Свойства 7), 8) называются законами поглощения, свойства 9) – 14) – законами правой дистрибутивности операций умножения, сложения, вычитания и декартова произведения (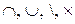), относительно операций сложения и умножения ().

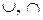Справедливость выписанных равенств следует непосредственно из определений операций над множествами и легко проверяется. Так, проверку равенства 12) можно записать в виде последовательности следующих утверждений:

.

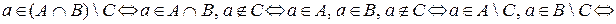
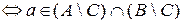По аналогии с объединением и пересечением двух множеств можно ввести объединение и пересечение произвольного семейства множеств :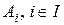

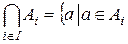для всех ,

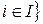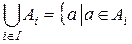хотя бы для одного .

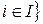В частности, если 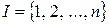, то вместо 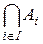, 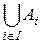пишут соответственно 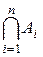, , 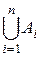или , .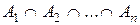

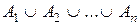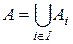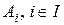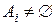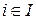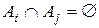Если имеет место равенство , то говорят, что множество А разложено в объединение своих подмножеств . Если при этом при всех и при 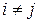, то говорят о разбиении множества А.