Пусть дано некоторое множество А, содержащее хотя бы один элемент. Будем говорить, что в множестве А определена алгебраическая операция, если указан закон, по которому любой паре элементов а и  , взятых из этого множества в определенном порядке, ставится во взаимно однозначное соответствие некоторый элемент с, также принадлежащий этому множеству. Если эту операцию называют сложением, то элемент с называют суммой элементов а и
, взятых из этого множества в определенном порядке, ставится во взаимно однозначное соответствие некоторый элемент с, также принадлежащий этому множеству. Если эту операцию называют сложением, то элемент с называют суммой элементов а и  и обозначают символом а +
и обозначают символом а +  ; если операцию называют умножением, то элемент с называется произведением элементов а и
; если операцию называют умножением, то элемент с называется произведением элементов а и  и обозначают символом а
и обозначают символом а  . В остальных случаях алгебраическую операцию будем обозначать символом *.
. В остальных случаях алгебраическую операцию будем обозначать символом *.
Алгебраическая операция * называется коммутативной, если результат ее применения не зависит от порядка элементов, т.е. для любых элементов а и  из рассматриваемого множества выполняется равенство
из рассматриваемого множества выполняется равенство 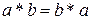 .
.
Алгебраическую операцию * называют ассоциативной, если для любых трех элементов а,  , с рассматриваемого множества выполняется равенство
, с рассматриваемого множества выполняется равенство 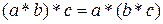 .
.
Если операция ассоциативна и коммутативна, то результат не зависит от порядка расположения элементов в этом выражении.
Для алгебраической операции * часто приходится рассматривать наличие обратной операции, что равносильно решению уравнений 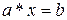 ,
, 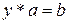 относительно элементов
относительно элементов 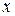 и
и 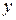 из множества А. Решение этих уравнений приводит к правой и левой обратным операциям. В случае их существования будем говорить, что операция * имеет обратную операцию. Наличие обратной операции равносильно существованию для любого элемента рассматриваемого множества правого и левого обратных элементов.
из множества А. Решение этих уравнений приводит к правой и левой обратным операциям. В случае их существования будем говорить, что операция * имеет обратную операцию. Наличие обратной операции равносильно существованию для любого элемента рассматриваемого множества правого и левого обратных элементов.
Если для элемента а правый и левый обратные элементы совпадают, то этот единственный элемент называют обратным элементом к элементу а. В случае, когда алгебраическая операция названа сложением, обратный элемент к элементу а называют противоположным элементом для элемента а и обозначают символом – а; в случае, когда алгебраическая операция названа умножением, обратный элемент к элементу а обозначается символом 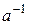 . Это позволяет операцию, обратную к умножению, записать в виде
. Это позволяет операцию, обратную к умножению, записать в виде 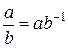 .
.
Пусть в множестве К введены две операции – операция сложения и операция умножения. Говорят, что эти операции связаны законом дистрибутивности, если для любых элементов а,  , с из К выполняются соотношения
, с из К выполняются соотношения 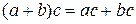 ,
, 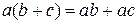 .
.
Группой называют множество с одной ассоциативной обратной операцией. Если алгебраическая операция в группе названа сложением, то группу называют аддитивной; если алгебраическая операция в группе названа умножением, то группу называют мультипликативной. Группу с коммутативной операцией называют абелевой; группу, состоящую из конечного числа элементов, называют конечной группой, а число элементов в группе – порядком группы.
Примерами групп являются:
1. Множество всех целых чисел с операцией сложения чисел.
2. Множество всех четных чисел с операцией сложения чисел.
3. Множество всех чисел, кратных данному числу п, с операцией сложения чисел.
4. Множества всех векторов на прямой, на плоскости и в пространстве с операцией сложения векторов.
Если дана какая-либо группа 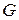 и подмножество Н, содержащееся в
и подмножество Н, содержащееся в 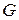 , образует группу относительно алгебраической операции, заданной в
, образует группу относительно алгебраической операции, заданной в 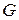 , то группу Н называют подгруппой группы
, то группу Н называют подгруппой группы 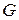 . Например, аддитивная группа всех четных чисел является подгруппой аддитивной группы всех целых чисел, которая сама является подгруппой аддитивной группы всех действительных чисел.
. Например, аддитивная группа всех четных чисел является подгруппой аддитивной группы всех целых чисел, которая сама является подгруппой аддитивной группы всех действительных чисел.
Множество К называют кольцом, если в нем определены ассоциативные операции сложения и умножения, связанные законом дистрибутивности, причем операция сложения коммутативная и обладает обратной операцией – вычитанием.
Кольцо называют коммутативным, если в нем операция умножения коммутативная, и некоммутативным – в противном случае. Заметим, что любое кольцо является абелевой группой по сложению.
Коммутативное кольцо Р, в котором есть единичный элемент и каждый ненулевой элемент имеет обратный элемент относительно умножения, называют полем.
Примерами полей являются:
1. Множество всех чисел вида 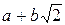 , где а и
, где а и  - рациональные числа, с операциями сложения и умножения.
- рациональные числа, с операциями сложения и умножения.
2. Множество, состоящее из двух элементов 0 и 1, с операциями сложения и умножения, заданными равенствами 0 + 0 = 0, 0 + 1 = 1 + 0 = 1, 1+1=0, и 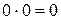 ,
, 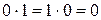 ,
, 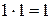 .
.
В любом поле множество всех элементов является абелевой группой с операцией сложения, а множество всех ненулевых элементов – абелевой группой с операцией умножения. Отсюда следует, что операции сложения и умножения имеют обратные операции – вычитание и деление. Для этих операций используют те же обозначения, что и для одноименных числовых операций. Кроме того, для четырех операций (сложение, умножение, вычитание, деление) сохраняются обычные правила преобразования выражений, а именно: 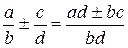 ,
, 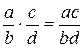 ,
, 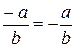 .
.
Перечислим нужные нам в дальнейшем общие факты об элементах произвольного поля.
В поле Р определена операция, называемая сложением, которая каждой паре элементов а и  поля Р ставит в соответствие элемент а +
поля Р ставит в соответствие элемент а +  из Р, называемый суммой элементов а и
из Р, называемый суммой элементов а и  . При этом:
. При этом:
1) сложение коммутативно, т.е. 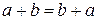 для любых элементов а и
для любых элементов а и  из Р;
из Р;
2) сложение ассоциативно, т.е. 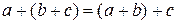 для любых элементов а,
для любых элементов а,  , с из Р;
, с из Р;
3) в поле Р существует единственный элемент 0, называемый нулевым, такой, что 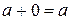 для любого элемента а из Р;
для любого элемента а из Р;
4) для любого элемента а из Р существует единственный элемент 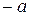 , называемый противоположным, такой, что
, называемый противоположным, такой, что 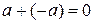 (это свойство обеспечивает существование операции, обратной к сложению, - вычитания).
(это свойство обеспечивает существование операции, обратной к сложению, - вычитания).
В поле Р определена операция, называемая умножением, которая каждой паре элементов а и  из Р ставит в соответствие элемент а
из Р ставит в соответствие элемент а  из Р, называемый произведением элементов а и
из Р, называемый произведением элементов а и  . При этом:
. При этом:
1) умножение коммутативно, т.е. 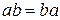 для любых элементов а и
для любых элементов а и  из Р;
из Р;
2) умножение ассоциативно, т.е. 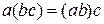 для любых элементов а,
для любых элементов а,  , с из Р;
, с из Р;
3) в поле Р существует единственный элемент 1, называемый единичным, такой, что 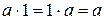 для любого элемента а из Р;
для любого элемента а из Р;
4) для каждого ненулевого элемента а из Р существует единственный элемент 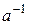 , называемый обратным, такой, что
, называемый обратным, такой, что 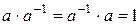 (это свойство обеспечивает существование в поле Р операции, обратной к умножению, - деление).
(это свойство обеспечивает существование в поле Р операции, обратной к умножению, - деление).
В поле Р сложение и умножение связаны законом дистрибутивности, т.е. для любых элементов а,  , с из Р выполняется соотношение
, с из Р выполняется соотношение 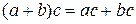 .
.
1 Определите понятие множества (способы задания; обозначение множества, элементов множества).
2 Равные множества, подмножество данного множества (определение, обозначение).
3 Пересечение множеств (определение, обозначение).
4 Перечислите свойства и операции пересечения множеств.
5 Дайте определение объединения множеств (обозначение, иллюстрация).
6 Перечислите свойства операции объединения множеств.
7 Дайте определение дополнения к множеству 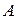 .
.
8 Перечислите свойства операции дополнения.
9 Определите разность двух множеств.
10 Дайте определение кортежа длины 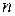 .
.
11 Какие два кортежа называются равными?
12 Определите отличия понятий кортежа и множества.
13 Определите декартовое произведение множеств.
14 Приведите примеры декартова произведения множеств.
15 Определите 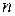 -мерное арифметическое пространство через декартово произведение.
-мерное арифметическое пространство через декартово произведение.
16 Что означает – декартовая 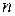 -ая степень множества
-ая степень множества 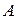 ?
?
17 Какие свойства операций над множествами называются законами поглощения?
18 Перечислите законы правой дистрибутивности операций умножения, сложения, вычитания и декартова произведения относительно операций сложения и умножения.
19 Осуществите проверку равенства 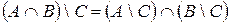 .
.
20 Что означает объединение и пересечение произвольного числа множеств?
21 Что означает высказывание «множество 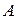 разложено в объединение своих подмножеств»?
разложено в объединение своих подмножеств»?
22 Сформулируйте определение отношения на множестве 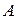 .
.
23 Приведите примеры отношений на множестве.
24 Какое отношение на множестве называется отношением эквивалентности?
25 Приведите примеры отношений эквивалентности.
26 Сформулируйте и докажите теорему об отношении эквивалентности.
27 Сформулируйте определение отображения множества 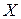 в множество
в множество 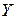 .
.
28 Что означает образ элемента, прообраз элемента в отображении 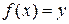 ?
?
29 Что означает – полный прообраз?
30 Какие виды отображений вы изучили?
31 Сформулируйте определение и приведите пример сюръективного отображения.
32 Сформулируйте определение и приведите пример инъективного отображения.
33 Сформулируйте определение и приведите пример биективного отображения.
34 Сформулируйте определение композиции отображений.
35 Сформулируйте и докажите свойства композиций отображений.
36 Что означает понятие алгебраическая операция?
37 Какая алгебраическая операция называется коммутативной?
38 Какая алгебраическая операция называется ассоциативной?
39 Что означает существование обратной алгебраической операции?
40 Сформулируйте определение обратного элемента к элементу 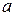 (для сложения, для умножения).
(для сложения, для умножения).
41 Сформулируйте определение группы.
42 Какая группа называется аддитивной?
43 Какая группа называется мультипликативной?
44 Какая группа называется абелевой?
45 Приведите примеры групп.
46 Сформулируйте определение кольца.
47 Какое кольцо называется коммутативным (некоммутативным)?
48 Сформулируйте определение поля.
49 Приведите примеры полей.
50 Перечислите операции, определенные в поле и их свойства.
 2015-05-22
2015-05-22 6191
6191







