Свойства операции объединения множеств

1) 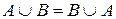- свойство коммутативности.

2) 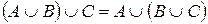- свойство ассоциативности.

3) Если 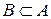, то .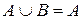

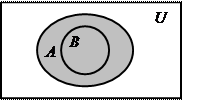Рисунок 7

4) , .

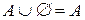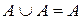5) 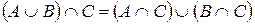- свойство дистрибутивности.

Проиллюстрируем свойство дистрибутивности на кругах Эйлера-Венна:

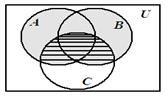
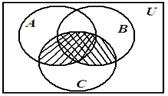
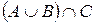
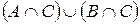
Рисунок 8

Докажем свойство дистрибутивности.

Определимся, для того, чтобы доказать равенство двух множеств, необходимо показать, что каждый элемент первого множества принадлежит второму и обратно – каждый элемент второго множества принадлежит первому.

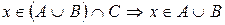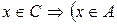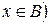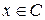
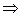
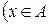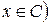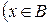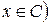
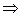
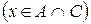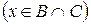
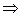
Пусть и или и и или и или - что и требовалось доказать.

Таким образом, всякий элемент х из левого множества одновременно принадлежит и правому множеству. Доказательство обратного утверждения предлагаем читателю выполнить самостоятельно.

Дополнение

Операция дополнения определена лишь в случае, когда все изучаемые множества рассматриваются как подмножества некоторого универсального множества U.

Пусть 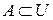. Дополнением к А называют множество всех элементов из U, не принадлежащих А. Дополнение обозначают : .

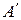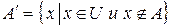Например, рассмотрим 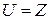- множество целых чисел и А – множество нечетных чисел. Тогда 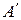есть множество четных чисел.

Или, например, пусть 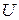- множество точек круга, а А – множество точек границы этого круга, (т.е. множество точек окружности), тогда 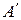- открытый круг.

Рисунок 9