Отношения на множествах

Прежде чем определить строго понятие отношения, приведем примеры отношений из школьной математики. Такими примерами могут служить отношения «меньше», «больше» на числовых множествах, отношения параллельности и перпендикулярности на множестве прямых плоскости, отношение подобия многоугольников, отношение равносильности систем уравнений относительно одних и тех же неизвестных и т.д. В каждом случае отношение позволяет выделять из всех пар элементов множества такие пары 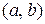, в которых а связано этим отношением с , например 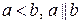и т.п. В связи с этим в общем случае принимается следующее определение:

Отношением на множестве А называется любое подмножество декартова квадрата 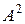множества А.

Пусть 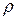- любое отношение на множестве А. Тогда для любого элемента а из А можно определить подмножество .

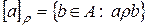Так, если 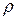есть отношение < на Z, то 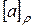есть множество всех целых чисел, больших, чем а. Если 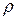- отношение параллельности, то 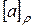есть множество всех прямых, параллельных прямой а, и т.д. Естественно возникает вопрос: для каких отношений 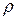на А все различные подмножества типа 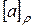образуют разбиение множества А?

Отношение 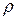на множестве 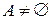называется отношением эквивалентности, если оно обладает следующими свойствами:

1) 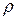- рефлексивно, т.е. 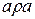для любого ,

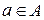2) 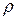- симметрично, т.е. 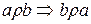для любых ,

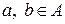3) 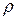- транзитивно, т.е. 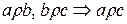для любых .

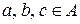В приведенных выше примерах отношениями эквивалентности являются отношения параллельности прямых, подобия многоугольников и равносильности систем уравнений.

Теорема Если 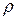есть отношение эквивалентности на множестве А, то все попарно различные подмножества типа 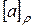образуют разбиение множества А.

Доказательство. Из определения соотношения эквивалентности видно, что 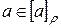, и поэтому каждое из множеств 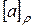не пусто и каждый элемент из А содержится хотя бы в одном из таких подмножеств. Остается доказать, что любые два подмножества 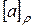, 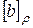либо совпадают, либо не пересекаются. Пусть 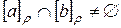, и 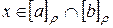. Тогда имеем соотношения: 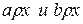. Из них, используя свойства симметричности и транзитивности, получим 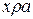и 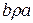. Если с – любой элемент из 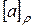, то имеем 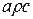, что вместе с 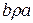приводит к соотношению 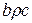. Следовательно, 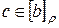, т.е. 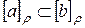. Аналогично доказывается и обратное включение. Таким образом, из наличия во множествах 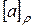, 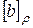одного общего элемента х следует их полное совпадение. Значит, различные подмножества типа 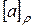либо совпадают, либо не пересекаются. Теорема доказана.

Если 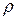есть отношение эквивалентности, то элементы, связанные отношением 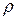, называются эквивалентными, а подмножества 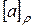- классами эквивалентности. Подчеркнем, что в этом случае все элементы одного класса эквивалентны между собой, а любые элементы из разных классов – не эквивалентны.