1) Вычислить: а) (3–2i)2+(1+3i)(–2+5i);
б) (2+3i)(4–5i)–(2–3i)(4+5i);
в) 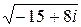 ;
;
г) 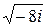 ;
;
д) 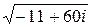 .
.
2) Решить уравнения:
а) x2–(2+i)x–1+7i=0;
б) x2–(3–2i)x+5–5i=0;
в) x4–3x2+4=0.
3) Представить в тригонометрической форме:
а) 2–2i; б) –3–i 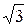 ; в) 5; г) –4; д) 3i.
; в) 5; г) –4; д) 3i.
4) Вычислить
а) 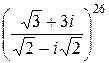 б)
б) 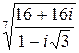 в)
в) 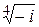
5) Решить уравнения:
а) x6+27=0; б) x8+x4+1=0.
§7. Уравнения третьей степени.
Уравнение третьей степени
x3+ax2+bx+c= 0 (1)
подстановкой x=y – 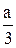 приводится к приведенному кубическому уравнению
приводится к приведенному кубическому уравнению
y3+py+q= 0. (2)
Корни такого уравнения можно найти по формулам Кардано:
y=u+v = 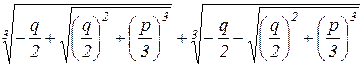 , (3)
, (3)
где
u = 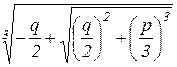 , v =
, v = 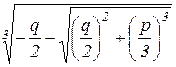
и они связаны соотношением
u×v = 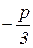 . (4)
. (4)
С учётом (4) формулу Кардано (3) можно использовать и в таком виде:
y=u 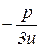 , где u =
, где u = 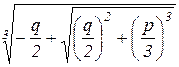 . (5)
. (5)
Здесь можно брать любое (одно из двух) значение квадратного корня; три значения кубического корня дают три корня приведенного уравнения (2). Заметим, что u ¹0, если p ¹0; если p =0, то никакая специальная формула не нужна (имеем двучленное уравнение).
Чтобы не запоминать формулу, можно пользоваться методом решения, по сути повторяющим вывод формул Кардано. Чтобы найти корни уравнения (2) (считаем р ¹0), пологая y=u+v, подставляем его в уравнение:
(u + v)3+ p (u + v)+ q =0.
Раскрыв скобки, и перегруппировав члены, получим:
(u 3+ v 3+ q)+(3 uv + p)(u + v)=0.
Для уничтожения второго слагаемого подберём u, v так, чтобы 3 uv + p =0 или u×v = 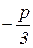 . Тогда уравнение (2) приводится к системе уравнений:
. Тогда уравнение (2) приводится к системе уравнений:


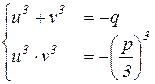
Замечаем, что u 3, v 3 – корни квадратного уравнения
z2+qz 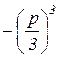 =0.
=0.
Затем, выбираем один (любой) корень z 1 этого квадратного уравнения. Берём в качестве u1 одно (любое) значение кубического корня из z 1 и вычисляем корни кубического уравнения (1) по следующей схеме:
u 1, v 1= 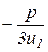 , y1=u1+v1, x1=y1 –
, y1=u1+v1, x1=y1 – 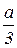 ;
;
u 2= u1e1, v 2= v1e2, y2=u2+v2, x2=y2 – 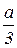 ;
;
u 3= u1e2, v 3= v1e1, y3=u3+v3, x3=y3 – 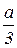 ;
;
где e1,2= 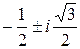 невещественные кубические корни из единицы. Заметим, что e2=(e1)2=
невещественные кубические корни из единицы. Заметим, что e2=(e1)2= 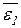 и e1=(e2)2=
и e1=(e2)2= 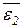 , это позволяет варьировать нахождение u 2, v 2, u 3, v 3.
, это позволяет варьировать нахождение u 2, v 2, u 3, v 3.
При исследовании уравнений третьей степени используют теорему:
Теорема. Пусть x3+px+q= 0 неполное кубическое уравнение с действительными коэффициентами. Обозначим
∆= 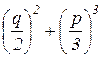 .
.
1. Если ∆>0, то уравнение имеет один действительный и два мнимых сопряжённых корня.
2. Если ∆=0, то корни уравнения действительны и хотя бы один из них кратный.
3. Если ∆<0, то все корни действительны и различны.
Если не все коэффициенты уравнения (2) действительны, то для упрощения вычислений можно вычислить ∆. Если ∆=0 (p ¹0, q ¹0), тогда уравнение (2) имеет два равных корня y2=y3, и в этом случае корни уравнения (2) можно найти, не прибегая к извлечению корней второй и третьей степени, а именно
y1 = 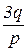 ; y2 = y3 =
; y2 = y3 = 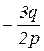 . (6)
. (6)
Если же ∆¹0, то уравнение (2) имеет три различных корня, для нахождения которых, используют один из вышеописанных способов.
Пример 1. Решить уравнение:
x3–6x +9=0.
Решение. Уравнение приведенное (отсутствует член с x 2). Используем модифицированную формулу Кардано (5):
∆= 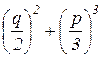 =
= 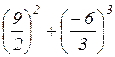 =
= 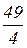 >0.
>0. 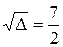
(берём только одно значение квадратного корня). Тогда
u = 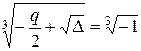 .
.
Одно из значений 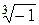 есть u 1=–1, ещё два значения получим, умножая u 1 на
есть u 1=–1, ещё два значения получим, умножая u 1 на
e1,2 – кубические корни из единицы. Итак,
u 1=–1, x1= u1 – 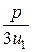 = – 1–
= – 1– 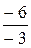 =–3;
=–3;
u 2= u1e1=–e1, x2= u2 – 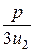 = –e1+
= –e1+ 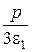 =– e1–2/e1=
=– e1–2/e1=
=– e1–2e2= 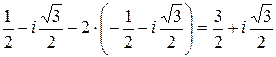 .
.
Так как коэффициенты данного уравнения действительны и ∆>0, то x 3= 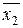 (x 3 не нужно вычислять по формуле).
(x 3 не нужно вычислять по формуле).
Ответ: x1= –3, x 2,3= 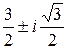 .
.
Пример 2. Решить уравнение:
x3+9x2+18x +28=0.
Решение. Сделаем подстановку x=y – 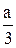 = y –3. Получим уравнение
= y –3. Получим уравнение
y3–9y+28= 0.
Полагаем y=u+v:
(u+v)3–9(u+v)+28=0,
(u 3+ v 3+28)+(3 uv –9)(u+v)=0.
Откуда 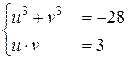 , или
, или 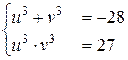 , где u 3, v 3 – корни квадратного уравнения
, где u 3, v 3 – корни квадратного уравнения
z2+28z +27=0.
Один из корней последнего уравнения z 1=–1, тогда
u 1=–1, v 1= 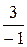 =–3, y1=–4, x1= –7;
=–3, y1=–4, x1= –7;
u 2= u1e1 = 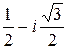 , v 2= v1e2=
, v 2= v1e2= 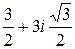 , y2=
, y2= 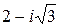 , x2=
, x2= 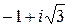 ;
;
Поскольку коэффициенты уравнения действительны и ∆>0, то x 3= 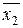 .
.
Ответ: x1= –7, x 2,3= 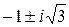 .
.
Пример 3. Решить уравнение:
x3+3x –2 i =0.
Решение. Данное уравнение приведенное, и не все его коэффициенты действительны, поэтому вычислим ∆.
∆= 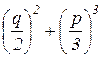 =
= 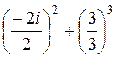 =–1+1=0
=–1+1=0
Таким образом корни уравнения можно вычислить по формулам (6).
x1 = 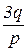 =
= 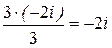 ; x2 = x3 =
; x2 = x3 = 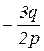 =
= 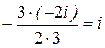 .
.
Ответ: x1= –2 i, x 2,3= i.
Пример 4. Решить уравнение:
x3–3abx+ a3+b3 =0
Решение. Пологая x=u+v, получим
(u+v)3–3ab(u+v)+ a3+b3 =0 или (u 3+ v 3+ a3+b3)+(3 uv –3 ab)(u+v)=0.
Откуда 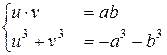
Одно из решений последней системы
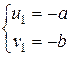
Тогда
u 1=– a, v 1=– b, x1= – a–b;
u 2= u1e1 = 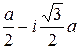 , v 2= v1e2=
, v 2= v1e2= 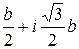 , x2=
, x2= 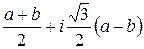 .
.
Ответ: x1= – a–b, x 2,3= 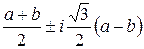 .
.
Замечание: При выписывании ответа воспользовались тем, что при вещественных a,b не надо вычислять x 3. Но если выписанное значение x 3 есть корень уравнения при (любых) вещественных a и b, то ясно, что x 3 будет корнем при любых a,b.
Для самостоятельного решения.
Решить уравнения:
1. x3+6x2–12x +32=0
2. x3+9x2–18x +44=0
3. x3–3x2–6x +36=0
4. x3–12x2+24x –40=0
5. x3–6ix +4(1– i)=0
6. x3+(3–3i 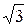 )x –9=0
)x –9=0
7. x3+3ax +1– a3 =0
Ответы:
1. (–8; 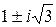 )
)
2. (–11; 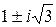 )
)
3. (–3; 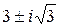 )
)
4. (10; 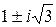 )
)
5. (2+2 i; –1– i; –1– i)
6. (i 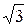 ;
; 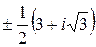

7. (a –1; 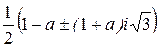
§8. Уравнения четвёртой степени.
Уравнение четвёртой степени
x 4+ ax 3+ bx 2+ cx + d =0 (1)
можно решить методом Феррари. Левая часть уравнения (1) раскладывается на два множителя второй степени, которые последовательно приравниваются к нулю. Для нахождения такого разложения левую часть представляют как разность квадратов.
Рассмотрим один из вариантов разложения левой части (4) на множители. Перенесём три последних члена уравнения (1) в правую часть. Тогда уравнение (1) перепишем в виде
x 4+ ax 3 =– bx 2– cx – d | + a 2 x 2/4
и прибавим к обеим частям уравнения a 2 x 2/4,для того, чтоб получить в правой части полный квадрат:
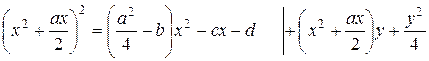 .
.
Прибавим к обеим частям полученного уравнения выражение
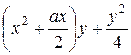 , зависящее от параметра y, чтобы получить в обеих частях уравнения полные квадраты:
, зависящее от параметра y, чтобы получить в обеих частях уравнения полные квадраты:
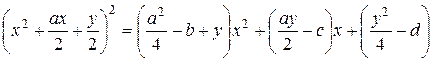 . (2)
. (2)
Правая часть уравнения будет полным квадратом, если, рассматривая её как уравнение второй степени
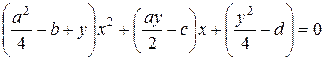 ,
,
она будет иметь два совпадающих корня, т. е. когда дискриминант этого уравнения равен нулю:
D= b 2–4 ac =0Û 
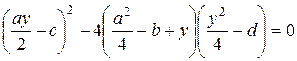 . (*)
. (*)
Чтоб найти y нужно решить уравнение третей степени (*). При этом достаточно найти хоть один корень y0. Подставим его в уравнение (2), которое преобразуется в
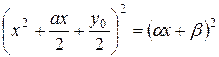 .
.
Откуда
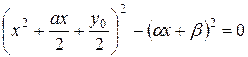
или
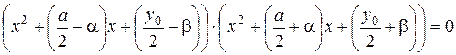
Левая часть (3) представляет разложение левой части (1) на множители. Из (3) имеем
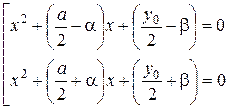 . (3)
. (3)
Решая квадратные уравнения (3), найдём все четыре корня исходного уравнения (1). Итак, решение уравнения четвёртой степени сводится к решению одного уравнения третей степени и двух уравнений второй степени.
Пример 1. Решить уравнение:
x 4+2 x 3+5 x 2+6 x +9=0
Решение. Переносим в правую часть уравнения все члены, степень которых не превышает двух:
x 4+2 x 3=–5 x 2–6 x –9.
Если к обеим частям последнего уравнения прибавить a 2 x 2/4= x 2, то в левой части получится полный квадрат:
(x 2+ x)2=–4 x 2–6 x –9.
Теперь к обеим частям получившегося уравнения прибавляем (x 2+ x) y +1/4× y 2. От этого левая часть не перестанет быть полным квадратом и примет вид:
(x 2+ x+ 1/2× y)2 = (y– 4) x 2+(y– 6) x +(1/4× y 2–9) (*)
Возьмём теперь y таким, чтобы и правая часть уравнения (*) стала полным квадратом. Для этого потребуем, чтобы
D= b 2–4 ac =0Û (y– 6)2–4(y– 4) (1/4× y 2–9)=0Û(y– 6)2– (y– 4) (y 2–36)=0.
 Замечаем, что одним из корней является y 0=6. Подставим его в (*). Получим
Замечаем, что одним из корней является y 0=6. Подставим его в (*). Получим
(x 2+ x+ 3)2 =2 x 2.
Это уравнение распадается на два квадратных уравнения:
x 2+(1+ 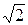 ) x+ 3 =0
) x+ 3 =0
x 2+(1– 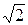 ) x+ 3 =0.
) x+ 3 =0.
Решая квадратные уравнения, получаем все четыре корня данного уравнения четвёртой степени:
x1,2= 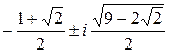 ,
,
x3,4= 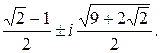
Ответ: x1,2= 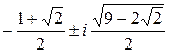 , x3,4=
, x3,4= 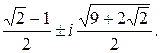
Пример 2. Решить уравнение:
x 4–2 x 3–6 x 2–26 x –15=0
Решение.
x 4–2 x 3=6 x 2+26 x +15 | + x 2 Û
Û (x 2– x)2=7 x 2+26 x +15 | +(x 2– x) y+y 2/4 Û
Û (x 2– x+y/ 2)2=(7+ y) x 2+(26– y) x +(15 +y 2/4) (*)
Возьмём теперь y таким, чтобы и правая часть уравнения (*) стала полным квадратом. Для этого потребуем, чтобы
D= b 2–4 ac =0 Û (26– y)2–4(7+ y)(15 +y 2/4)=0 Û
Û y 3+6 y 2+112 y –256=0.
 Замечаем, что одним из корней является y 0=2. Подставим его в (*). Получим
Замечаем, что одним из корней является y 0=2. Подставим его в (*). Получим
(x 2– x+ 1)2=9 x 2+24 x+ 16 Û (x 2– x+ 1)2=(3 x +4)2
Это уравнение распадается на два квадратных уравнения:
x 2–4 x– 3=0,
x 2+2 x+ 5=0.
Решая квадратные уравнения, получаем все четыре корня данного уравнения четвёртой степени:
x1,2= 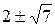 ,
,
x3,4= –1 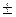 2 i.
2 i.
Ответ: x1,2= 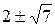 , x3,4= –1
, x3,4= –1 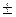 2 i.
2 i.
Пример 3. Решить уравнение:
x 4–2 x 3+2 x 2+4 x –8=0
Решение.
x 4–2 x 3+2 x 2+4 x –8=0 Û
Û x 4–2 x 3=–2 x 2–4 x +8 | + x 2Û
Û (x 2– x)2=– x 2–4 x +8 |+(x 2– x) y+y 2/4 Û
Û (x 2– x+y/ 2)2=(y– 1) x 2+(–4– y) x +(8 +y 2/4) (*)
Возьмём теперь y таким, чтобы и правая часть уравнения (*) стала полным квадратом. Для этого потребуем, чтобы
D= b 2–4 ac =0 Û (–4– y)2–4(y– 1)(8 +y 2/4)=0 Û
Û y 3–2 y 2+24 y –48=0.
 Замечаем, что одним из корней является y 0=2. Подставим его в (*). Получим
Замечаем, что одним из корней является y 0=2. Подставим его в (*). Получим
(x 2– x+ 1)2= x 2–6 x+ 9 Û (x 2– x+ 1)2=(x –3)2.
Это уравнение распадается на два квадратных уравнения:
x 2–2 x +4=0,
x 2–2 =0.
Решая квадратные уравнения, получаем все четыре корня данного уравнения четвёртой степени:
x1,2= 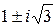 ,
,
x3,4= 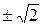 .
.
Ответ: x1,2= 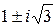 , x3,4=
, x3,4= 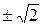 .
.
 2015-05-25
2015-05-25 1491
1491
