Задача 1. Вычислить определитель
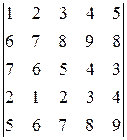 =∆
=∆
Решение. 1 способ. Получаем нули в первой строке определителя ∆, т.е. аннулируем все элементы первой строки, кроме первого, прибавляя ко второму, третьему, четвёртому и пятому столбцам первый, умноженный на (–2), (–3), (–4),
(–5) соответственно:
∆= 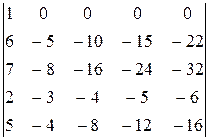
По свойству 7 определитель не изменится. Разложим его по первой строке
∆=1.(–1)1+1 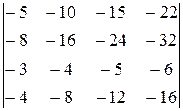 .
.
Аналогично преобразуем четвёртую строку
∆= 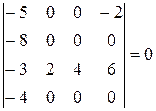 .
.
Определитель равен нулю, т.к. вторая и четвёртая строки пропорциональны.
2 способ. Заметим, что элементы соседних столбцов определителя отличаются друг от друга на единицу. Для общего уменьшения элементов определителя, вычтем из пятого столбца четвёртый, затем из четвёртого третий и т.д.
∆= 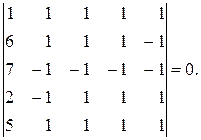
Определитель равен нулю, т.к. четвёртый и третий столбцы равны.
Ответ: ∆=0.
Задача 2. Вычислить определитель
∆= 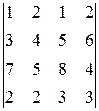 .
.
Решение. Получаем нули в первой строке и раскладываем по ней определитель
∆= 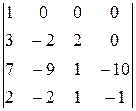 =1.(–1)1+1
=1.(–1)1+1 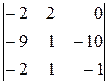 .
.
Ко второму столбцу полученного определителя прибавляем первый:
∆= 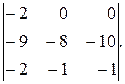
Разложим определитель по первой строке:
∆=–2.(–1)1+1 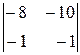 =–2(8–10)=4.
=–2(8–10)=4.
Ответ: ∆=4.
Задача 3. Найти определитель разложением по столбцу:
∆= 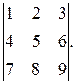
Решение. Разложим определитель по элементам первого столбца:
∆=1.(–1)1+1 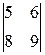 +4.(–1)2+1
+4.(–1)2+1 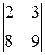 +7.(–1)3+1
+7.(–1)3+1 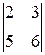 =(45–48)–4(18–24)+7(12–15)=0
=(45–48)–4(18–24)+7(12–15)=0
Ответ: ∆=0.
Задача 4. Вычислить матрицы, обратные данным, с помощью определителей:
а) А = 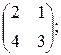 б) В =
б) В = 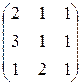 .
.
Решение. а) Найдём определитель матрицы А
∆=| А |= 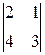 =2×3–1×4=6–4=2¹0.
=2×3–1×4=6–4=2¹0.
Определитель матрицы А отличен от нуля, поэтому матрица А невырожденная и для неё существует обратная матрица А–1, которую мы вычислим по формуле:
А–1= 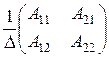
Найдём алгебраические дополнения матрицы А:
А11=(–1)1+1.3=3; А21=(–1)2+1.1=–1;
А12=(–1)1+2.4=–4; А22=(–1)2+2.2=2.
Тогда
А –1 = 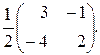
Сделаем проверку:
А×А –1= 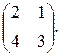
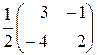 =
=
= 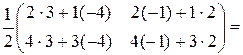
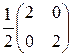 =
= 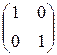 = Е.
= Е.
Замечание. Из сказанного выше, получаем формулу для обращения невырожденной матрицы второго порядка:
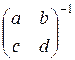 =
= 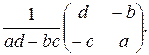
Для определителя третьего порядка приведенные вычисления усложняются и имеют только теоретическое применение.
б) Вычислим определитель матрицы В:
∆=| В |= 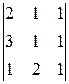 =
= 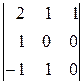 =1(–1)2+1
=1(–1)2+1 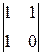 =–(0–1)=1¹0
=–(0–1)=1¹0
Матрица В невырожденная, поэтому для неё существует обратная В–1, которую вычислим по формуле:
В –1= 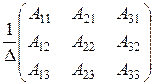 .
.
Найдём алгебраические дополнения элементов матрицы В:
А11=(–1)1+1 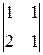 =–1; А21=(–1)2+1
=–1; А21=(–1)2+1 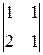 =1; А31=(–1)3+1
=1; А31=(–1)3+1 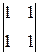 =0;
=0;
А12=(–1)1+2 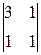 =–2; А22=(–1)2+2
=–2; А22=(–1)2+2 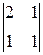 =1; А32=(–1)3+2
=1; А32=(–1)3+2 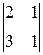 =1;
=1;
А13=(–1)1+3 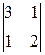 =5; А23=(–1)2+3
=5; А23=(–1)2+3 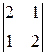 =–3; А33=(–1)3+3
=–3; А33=(–1)3+3 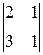 =–1.
=–1.
Тогда
В –1= 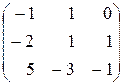 .
.
Проверка:
B×В– 1= 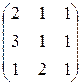 ×
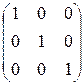
× 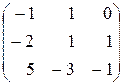 =
= 
Ответ: а) А –1=  б) В– 1=
б) В– 1= 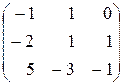 .
.
Задача 5. Решить систему линейных уравнений методом Крамера:

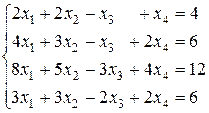
Решение. Находим определитель основной матрицы системы
∆= 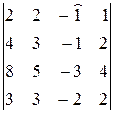 =
= 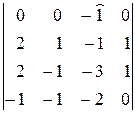 =(–1)(–1)1+3
=(–1)(–1)1+3 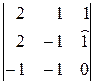 =–
=– 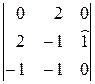 =
=
=(–1)(–1)2+3 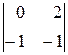 =0(–1)–(–1)2=2¹0
=0(–1)–(–1)2=2¹0
Определитель ∆¹0, поэтому система совместна определена и её единственное решение можно найти по формулам Крамера:
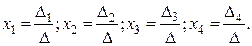
Вычислим четыре вспомогательных определителя, заменяя столбцом свободных членов поочерёдно столбцы основного определителя:
∆1= 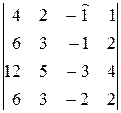 =
= 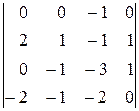 =(–1)(–1)1+3
=(–1)(–1)1+3 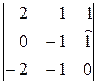 =
=
=– 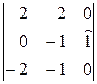 =(–1)(–1)2+3
=(–1)(–1)2+3 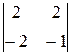 =–2+4=2;
=–2+4=2;
∆2= 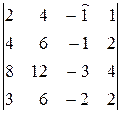 =
= 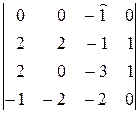 =(–1)(–1)1+3
=(–1)(–1)1+3 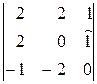 =
=
=– 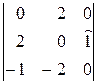 =(–1)(–1)2+3
=(–1)(–1)2+3 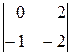 =2;
=2;
∆3= 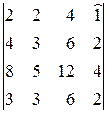 =
= 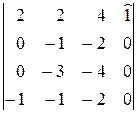 =1(–1)1+4
=1(–1)1+4 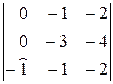 =
=
=–(–1)(–1)3+1 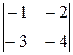 =4–6=–2;
=4–6=–2;
∆4= 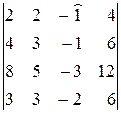 =
= 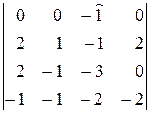 =(–1)(–1)1+3
=(–1)(–1)1+3 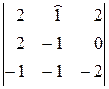 =
=
=– 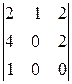 =(–1)(–1)1+2
=(–1)(–1)1+2 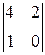 =–2;
=–2;
Итак х 1=2/2=1, х 2=2/2=1, х 3=–2/2=–1, х 4=–2/2=1.
Проверка:
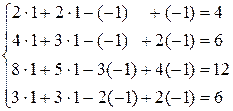
Ответ: {(1;1;–1;–1)}.
Для самостоятельного решения.
1. Методом Крамера решить системы линейных уравнений:
а) 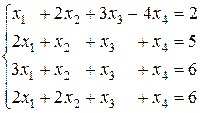 б)
б) 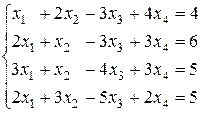 .
.
2. Вычислить матрицы, обратные данным, с помощью алгебраических дополнений:
а) 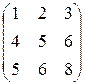 ; б)
; б) 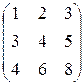 ; в)
; в) 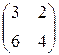 ; г)
; г) 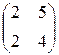 .
.
 2015-05-25
2015-05-25 1655
1655
