Задача 1. Вычислить:
1) (2+3i)+(5–7i); 2) (4+i)–(7+2i); 3) (3+2i)(5–2i); 4) (2+i)/(1+3i).
Решение. Пользуясь обычными свойствами действий: коммутативностью, ассоциативностью, дистрибутивностью, получим:
1) (2+3i)+(5–7i)=(2+5)+(3–7i)= 7–4i;
2) (4+i)–(7+2i)=(4–7)+(1–2)i=–3–i;
3) (3+2i)(5–2i)=3×5+2i×5–3×2i–(2i)2=15+10i–6i–4(–1)= 19+4i; (i2=–1);
4) 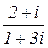 =
= 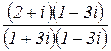 =
= 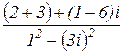 =
= 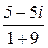 =
= 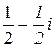 .
.
Ответ: 1) 7–4i; 2) –3–i; 3) 19+4i; 4) 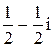 .
.
Задача 2. Найти действительные корни уравнения:
(2+i)x+(1–i)y=5–2i.
Решение. Преобразуем левую часть уравнения, следующим образом:
(2x+y)+(x–y)i=5–2i.
Учитывая единственность представления комплексного числа и то, что x,yÎR, имеем
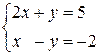 Û∆=
Û∆= 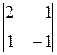 =–3; ∆1=
=–3; ∆1= 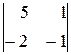 =-3; ∆2=
=-3; ∆2= 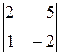 =–9.
=–9.
Откуда x=∆1/∆=1; y=∆2/∆=3.
Ответ: (1;3).
Задача 3. Вычислить 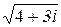
Решение. Пусть w – искомое число. Тогда по определению квадратного корня 4+3i =w2. Если w= х+yi, x,yÎR, то
4+3i=(х+yi)2 или 4+3i=(x2–y2)+2xyi
Откуда, т.к. x,yÎR, получим
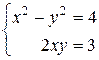 (1)
(1)
Возведя в квадрат оба уравнения системы (1), и сложив их, выведем следствие системы (1):
x2+2x2y2+y2=25, (2)
которое преобразуется к виду (x2+y2)2=25. Поэтому на множестве пар действительных чисел уравнение (2) равносильно уравнению (3):
x2+y2=5 (3)
Если в систему уравнений включить её следствие, то получится система, равносильная исходной. Включим уравнение (3) в систему (1):
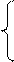
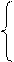
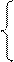 x2+y2=5 2x2=9 x2=9/2
x2+y2=5 2x2=9 x2=9/2
x2–y2=5 Û 2y2=5 Û y2=1/2
2xy=3 2xy=3 xy=3/2
Итак, система (1) имеет два решения: 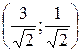 и
и 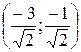 . Они дают два значения корня: w1=
. Они дают два значения корня: w1= 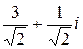 , w2=
, w2= 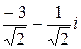 .
.
Ответ: 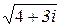 =
= 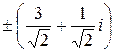 .
.
Задача 4. Решить уравнение:
x2–(2+i)x+(–1+7i)=0
Решение. Воспользуемся формулой вычисления корней квадратного уравнения
x1,2 = 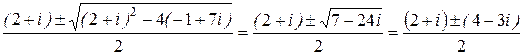 ,
,
откуда x1=3–i, x2=–1+2i.
Ответ. {3–i; –1+2i}.
Замечание. Квадратный корень из числа 7–24i извлекается как в задаче 3.
Задача 5. Вычислить in, где nÎZ.
Решение. Вычислим in для нескольких натуральных показателей: i0=1 (по определению), i1=i, i2=–1, i3=–i, i4=1, i5=i. Замечаем, что значения степени начинают повторяться: i4=i0, i5=i1, i6=i2, i7=i3,….Обобщим это наблюдение. Возьмём произвольное целое число n и поделим его с остатком на 4:
n=4k+r, k,rÎZ, 0£r<4.
Тогда in=i4k+r=(i4)k×ir= ir, так как i4=1. Значения ir для 0£r<4 уже найдены. Итак,
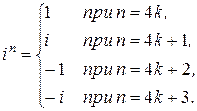
Задача 6. Решить систему уравнений
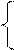 (2+i)x–(3–i)y=i
(2+i)x–(3–i)y=i
(3+i)x+(2–i)y=i.
Решение. Вычислим основной и два вспомогательных определителя системы:
∆= 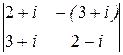 =(2+i)×(2–i)+(3+i)2=13+6i;
=(2+i)×(2–i)+(3+i)2=13+6i;
∆1= 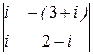 =i(2–i)+i(3+i)=2i+1+3i–1=5i;
=i(2–i)+i(3+i)=2i+1+3i–1=5i;
∆2= 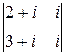 =2i–1–3i+1=–i.
=2i–1–3i+1=–i.
Тогда x=∆1/∆= 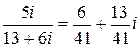 ; y=∆2/∆=
; y=∆2/∆= 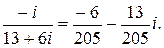
Ответ: 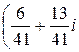 ;
; 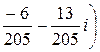 .
.
Задача 7. Представить в тригонометрической форме:
1) 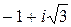 ; 2)–7i 3) 1+cosj+isinj.
; 2)–7i 3) 1+cosj+isinj.
Решение.
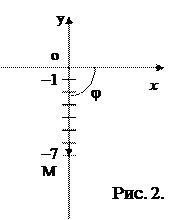 1) Найдём модуль r и аргумент j данного числа:
1) Найдём модуль r и аргумент j данного числа:
r= 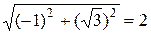 ; tgj=
; tgj= 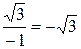 Þ(j=–p/3 или j=2p/3). Таким образом,
Þ(j=–p/3 или j=2p/3). Таким образом, 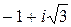 =2(cos
=2(cos 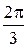 +i×sin
+i×sin 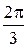 ).
).
2) На комплексной плоскости число (–7i) изображается радиус–вектором 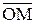 =(0;–7). Тогда
=(0;–7). Тогда
|–7i|=| 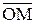 |=7, arg(–7i)=ÐXOM=–p/2. Итак,
|=7, arg(–7i)=ÐXOM=–p/2. Итак,
(–7i)= 7(cos(–p/2)+isin(–p/2)).
3) Преобразуем данное число:
1+cosj+isinj=2cos2(j/2)+i[2sin(j/2)×cos(j/2)]=
=2cos(j/2)[cos(j/2)+isin(j/2)].
Если cos(j/2)>0, то это и есть искомая тригонометрическая форма. Если же cos(j/2)<0, то внесём (–1) внутрь скобок:
2cos(j/2)[cos(j/2)+isin(j/2)]=–2cos(j/2)[cos(j/2+p)+isin(j/2+p)]
Ответ: 1) 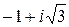 =2(cos
=2(cos 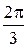 +i×sin
+i×sin 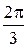 );
);
2)–7i=7(cos(–p/2)+isin(–p/2));
3) 1+cosj+isinj= 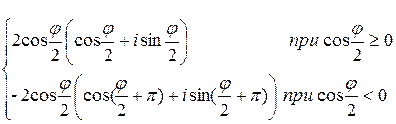 .
.
Задача 8. Вычислить:
1) 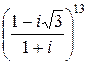 ; 2)
; 2) 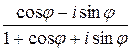 ;
;
Решение.
1) Представим числа, стоящие в числителе и знаменателе дроби в тригонометрической форме, для этого найдём модули и аргументы числителя и знаменателя.
a= 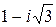 , |a|=
, |a|= 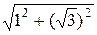 =2, arga=–p/3 (см. задачу 7, п.1).
=2, arga=–p/3 (см. задачу 7, п.1).
b=1+i, |b|= 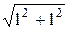 =
= 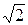 , argb=p/4.
, argb=p/4.
Выполняя операцию деления, получим:
a /b= 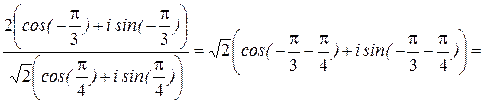
= 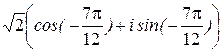 .
.
К полученному выражению применим формулу возведения тригонометрической формы комплексного числа в степень (формулу Муавра):
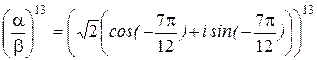 = =
= = 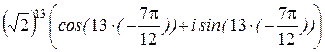 = =
= = 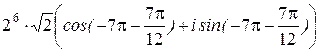 = =
= = 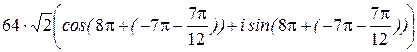 =
= 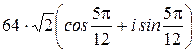 .
.
Замечание 1. Запись вычислений можно вести так:
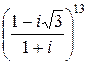 =
= 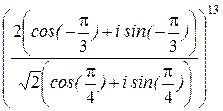 =
= 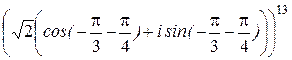 = =
= = 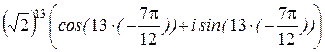 = =
= = 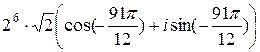 =
= 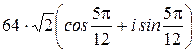 .
.
2). Задачу можно решить в алгебраической форме.
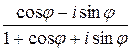 =
= 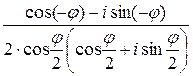 =
= 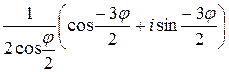
Замечание. 1) Используем результат задачи 7, п.3.
2) Знак сos(j/2) может быть любым, так как результат не обязательно получать в тригонометрической форме.
3) Ответ можно записать и так: 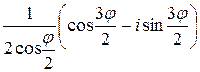 .
.
Ответ: 1) 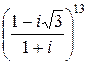 =
= 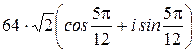 ;
;
2) 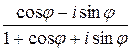 =
= 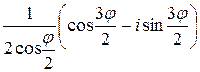 .
.
Задача 9. Найти все корни:
1) 5-ой степени из a= 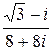 ;
;
2) 6-ой степени из 1+cosj+isinj;
3) 3-тей степени из i.
Решение. 1) Запишем a в тригонометрической форме:
a= 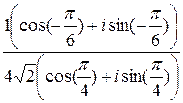 =
= 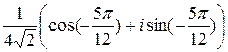 .
.
Воспользуемся формулой извлечения корня n-ой степени из тригонометрической формы комплексного числа:
wk = 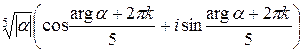 , k=0..4.
, k=0..4.
Найдём
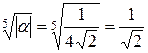 ,
, 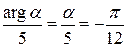 .
.
Все искомые корни задаются формулой
wk= 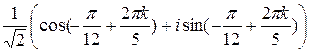 , k=0..4.
, k=0..4.
2) Воспользуемся результатом задачи 7, п.3. В данном случае, чтобы можно было воспользоваться формулой, необходима тригонометрическая форма подкоренного выражения (арифметический корень по определению существует только из положительного числа). Ответ получаем сразу:
wk = 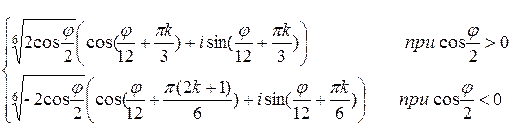 ,
,  k=0..5,
k=0..5,
w=0 при 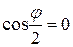 .
.
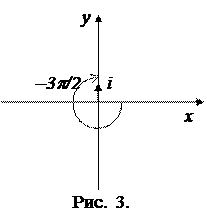 3) В качестве значения arg i выбираем то, которое делится на 3: из рис. 3
3) В качестве значения arg i выбираем то, которое делится на 3: из рис. 3
arga=–3p/2. Так как |i|=1, то одним из искомых корней будет:
w0=cos(–p/2)+i×sin(–p/2)=–i.
Остальные корни найдём, умножая w0 на корни 3-й степени из 1, т.е. на ek= 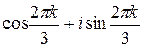 , k=0..2. Найдём
, k=0..2. Найдём 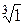 : e0=
: e0= 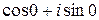 =1; e1=
=1; e1= 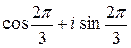 =
= 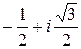 ; e2=
; e2= 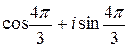 = =
= = 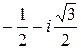 .
.
Тогда
wk=ek×w0, т.е. ×w0=–i, ×w1= 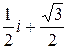 , ×w2=
, ×w2= 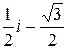 .
.
Ответ. 1) wk= 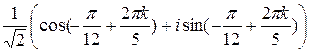 , k=1..4;
, k=1..4;
2) wk = 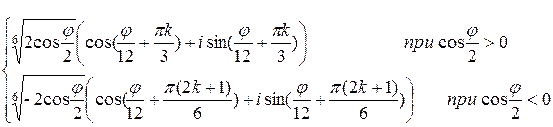 ;k=0..5,
;k=0..5,
w=0, при 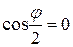 .
.
3) w0=–i, w1= 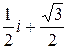 , w2=
, w2= 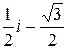 .
.
Задача 10. Решить уравнения:
1) x9+8=0; 2) x6+4x3+8=0.
Решение. 1) x9+8=0Û x9=–8. Корнями этого уравнения являются корни
9-той степени из (–8) и только они. Один из них равен 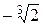 , все остальные корни получим, домножая его на все корни 9-ой степени из 1:
, все остальные корни получим, домножая его на все корни 9-ой степени из 1:
wk=w0×ek= 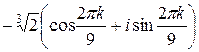 , k=0..8.
, k=0..8.
2) Используем подстановку y=x3, тогда уравнение примет вид:
y2+4y+8=0.
Корни квадратного уравнения
y1,2=–2 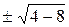 =–2±2i=2
=–2±2i=2 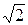 (
(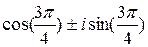 )
)
Извлекая кубический корень, получим ответ:
x1..6= 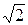
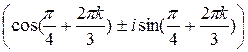 , k=0..2.
, k=0..2.
Замечание. Уравнение n-ой степени в поле комплексных чисел имеет в точности n решений (некоторые из которых могут совпадать). Поэтому указанное уравнение 6-ой степени имеет в точности 6 решений. Корни из числа cosj–isinj сопряжены с корнями из числа cosj+isinj, т.е. в формуле для корней нужно заменить i на (–i). Извлекать корни из y можно так: один из корней
w0= 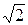
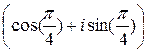 =
= 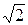
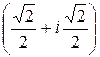 =1+i;
=1+i;
умножая его на корни 3-тей степени из единицы, получаем:
(1+i) 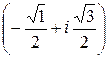
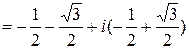 .
.
Аналогично находим остальные значения x. Окончательно получим:
x1,2= 1±i, x3,4= 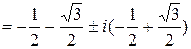 , x5,6=
, x5,6= 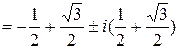 .
.
Ответ: 1) xk= 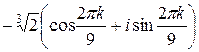 , k=0..8.
, k=0..8.
2) x1,2= 1±i, x3,4= 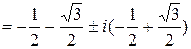 , x5,6=
, x5,6= 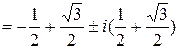 .
.
 2015-05-25
2015-05-25 5508
5508
