КОРДАНО.
Уравнение третьей степени с комплексными коэффициентами имеет вид:
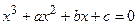 (1)
(1)
Без ограничения общности можно считать, что старший коэффициент равен единице; в противном случае мы поделили бы обе части уравнения на старший коэффициент.
Подвергнем (1) упрощению – сделаем член с квадратом неизвестного равным нулю, для чего положим 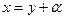 и найдем
и найдем 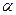 .
.
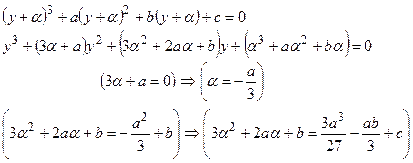
Таким образом, сделав в (1) подстановку 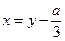 , получим неполное кубическое уравнение:
, получим неполное кубическое уравнение:
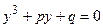 (2)
(2)
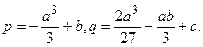
Чтобы найти корни уравнения (2), положим 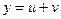 , где u и v – два новых вспомогательных неизвестных. (2) запишем в виде:
, где u и v – два новых вспомогательных неизвестных. (2) запишем в виде:
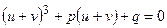 ,
,
раскрыв скобки и перегруппировав члены, получим:
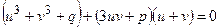 .
.
Потребуем, чтобы 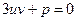 или
или 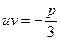 . Это требование всегда выполнимо, т.к. оно вместе с условием
. Это требование всегда выполнимо, т.к. оно вместе с условием 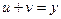 означает, что u и v являются корнями квадратного уравнения.
означает, что u и v являются корнями квадратного уравнения.
Тогда уравнение (2) приведется к уравнениям:
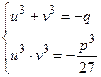
Отсюда 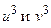 согласно формулам Виета являются корнями квадратного уравнения:
согласно формулам Виета являются корнями квадратного уравнения:
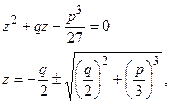
откуда
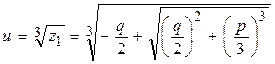
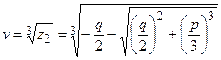 .
.
Итак, неполное уравнение (2) решено в радикалах:
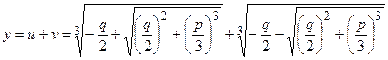 (3)
(3)
(3) – формула Кардана.
Формула Кардана состоит из суммы двух кубических радикалов. Каждый из них имеет три значения. Комбинируя значения u и v, получим девять сумм u+ v,но среди них только три корня уравнения (2). Это будут те суммы u+ v, у которых u и v связаны соотношением:
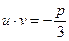 (4)
(4)
Обозначим через 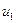 ,
, 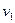 какую-нибудь пару значений
какую-нибудь пару значений 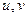 , удовлетворяющих (4), а через
, удовлетворяющих (4), а через 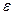 - один из первообразных корней третьей степени из единицы. Например:
- один из первообразных корней третьей степени из единицы. Например: 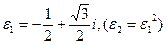 .
.
Тогда 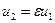 ,
, 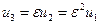 . Найдем
. Найдем 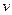 . Так как
. Так как 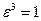 и
и 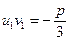 , то
, то
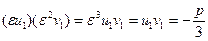 , откуда
, откуда 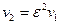
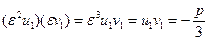 , откуда
, откуда 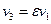 .
.
Таким образом, получим все значения корней неполного кубического уравнения (2):
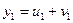 ,
, 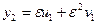 ,
, 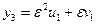 .
.
Учитывая, что 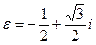 ,
, 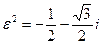 , имеем:
, имеем: 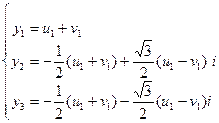 (5)
(5)
Пример. Определить по формуле Кардана корни уравнения: 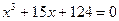
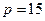 ,
, 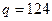 .
.
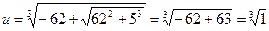
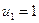 ,
, 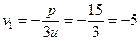
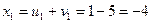
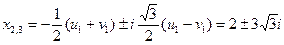
Обозначим 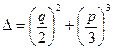 - выражение стоящее под знаком квадратного радикала в формуле Кардана.
- выражение стоящее под знаком квадратного радикала в формуле Кардана.
Предложение Если 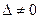 , то уравнение (2) имеет три различных корня.
, то уравнение (2) имеет три различных корня.
Покажем, что 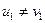 ,
, 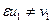 ,
, 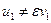 , где
, где 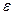 - первообразный корень третьей степени из 1.
- первообразный корень третьей степени из 1.
Пусть 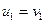 ,
, 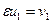 ,
, 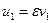 . Возведя обе части равенства в куб получим:
. Возведя обе части равенства в куб получим: 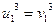 , т.е. квадратное уравнение
, т.е. квадратное уравнение 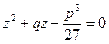 имеет два равных корня:
имеет два равных корня: 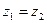 , что невозможно, т.к. дискриминант этого квадратного уравнения
, что невозможно, т.к. дискриминант этого квадратного уравнения 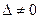 . Тогда из формул (5)
. Тогда из формул (5) 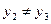 , т.к. при
, т.к. при 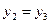
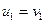 . Если бы
. Если бы 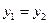 , то
, то 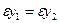 , т.е.
, т.е.
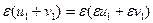
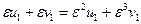
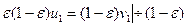
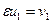 , что при
, что при 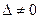 невозможно.
невозможно.
Аналогично обнаруживается, что 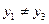 .
.
Если 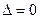 при
при 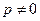 и
и 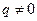 , то
, то 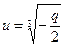
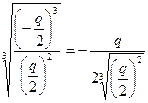 . Так как
. Так как 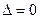 ,то
,то 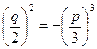 . Следовательно
. Следовательно 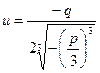 .
.
Откуда одно из значений 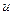 :
: 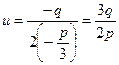 . Соответствующее значение
. Соответствующее значение 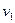 :
: 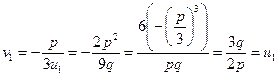
Обращаясь к формулам (5) получим: 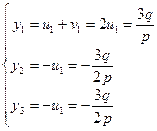
Предложение: При 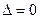 (
(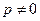 и
и 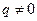 ) уравнение (2) имеет два равных корня:
) уравнение (2) имеет два равных корня: 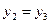 , и в этом случае корни (2) можно найти, не прибегая к извлечению корней второй и третьей степеней, а именно:
, и в этом случае корни (2) можно найти, не прибегая к извлечению корней второй и третьей степеней, а именно: 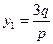 ,
, 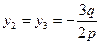 (6)
(6)
Пример: Решить уравнение: 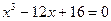 .
.
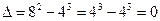
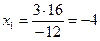
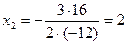
УРАВНЕНИЯ ТРЕТЬЕЙ СТЕПЕНИ С ДЕЙСТВИТЕЛЬНЫМИ КОЭФФИЦИЕНТАМИ.
Пусть 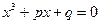
 (7) – неполное кубическое уравнение третьей степени с действительными коэффициентами и
(7) – неполное кубическое уравнение третьей степени с действительными коэффициентами и 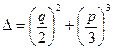 .
.
Теорема: Если 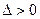 , то уравнение (7) имеет один действительный и два мнимых сопряженных корня;
, то уравнение (7) имеет один действительный и два мнимых сопряженных корня;
если 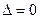 , то корни уравнения (7) действительны и хотя бы один из них кратный;
, то корни уравнения (7) действительны и хотя бы один из них кратный;
если 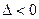 , то то все корни (7) действительны и различны.
, то то все корни (7) действительны и различны.
1. 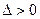 . Так как
. Так как 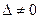 , то все три корня уравнения (7) должны быть различными.
, то все три корня уравнения (7) должны быть различными.
Рассмотрим выражение 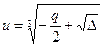 .
.
Так как 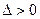 , то
, то 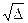 - действительное число. Следовательно, одно из значений и должно быть действительным. Пусть
- действительное число. Следовательно, одно из значений и должно быть действительным. Пусть 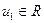 , тогда
, тогда 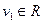 . На основании (5) уравнение (7) имеет только один действительный корень:
. На основании (5) уравнение (7) имеет только один действительный корень: 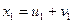 , а два остальных корня будут сопряженными чисто комплексными числами:
, а два остальных корня будут сопряженными чисто комплексными числами:
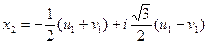 ,
,
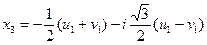 .
.
2. 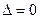 . При
. При 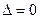 ,
, 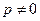 ,
, 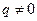 уравнение имеет два равных корня. Так как (7) уравнение с действительными коэффициентами, то при
уравнение имеет два равных корня. Так как (7) уравнение с действительными коэффициентами, то при 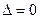 ,
, 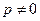 ,
, 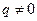 все три корня уравнения действительны, причем два из них равны.
все три корня уравнения действительны, причем два из них равны.
При 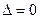 ,
, 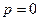 ,
, 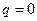 уравнение (7) имеет три равных нулю корня:
уравнение (7) имеет три равных нулю корня: 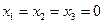 .
.
3. 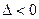 (неприводимый случай). Так как
(неприводимый случай). Так как 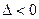 , то
, то 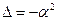 , где
, где 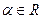 . Тогда
. Тогда 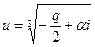 . Найдем модуль
. Найдем модуль 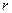 и аргумент
и аргумент 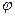 подкоренного выражения:
подкоренного выражения: 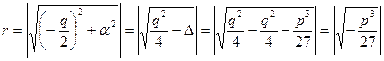
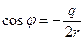 ,
, 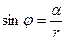 . Т.о.
. Т.о. 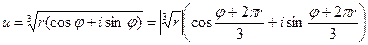 .
.
Полагая 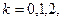 получим:
получим:
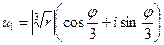
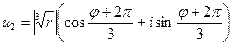
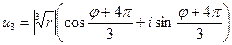 .
.
Произведение комплексного числа 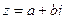 на сопряженное
на сопряженное 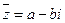 равно квадрату модуля
равно квадрату модуля 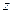 :
:
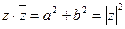 .
.
Найдем 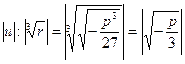
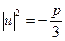 , т.е.
, т.е. 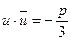 , но
, но 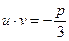 . Значит
. Значит 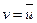 . Тогда
. Тогда
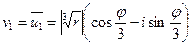
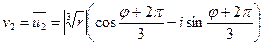
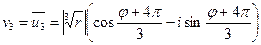
Тогда корни (7) имеют вид:
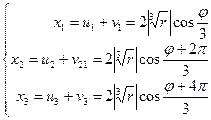 (8)
(8)
Итак, в случае 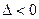 уравнение (7) имеет три действительных корня.
уравнение (7) имеет три действительных корня.
Недостаток формулы Кардана состоит в том, что она часто представляет рациональные корни в иррациональном виде.
Пример. 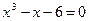 Очевидно
Очевидно 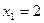 - действительный корень.
- действительный корень.
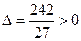 (один действительный и два сопряженных мнимых корня)
(один действительный и два сопряженных мнимых корня)
По формуле Кардана: 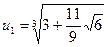
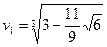 - иррациональные числа
- иррациональные числа
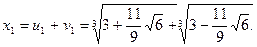
При приближенных вычислениях 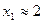 ,
, 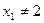 . Вследствие этого недостатка рациональные корни кубического уравнения с рациональными коэффициентами определяют не по формуле Кардана.
. Вследствие этого недостатка рациональные корни кубического уравнения с рациональными коэффициентами определяют не по формуле Кардана.
УРАВНЕНИЯ ЧЕТВЕРТОЙ СТЕПЕНИ.
Пусть 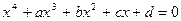 (1) –
(1) –
Уравнение четвертой степени с комплексными коэффициентами. Наиболее ранний способ решения (1) принадлежит Феррари ученику Кардана.
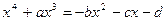
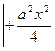
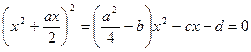
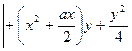
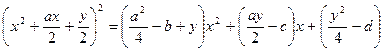 (2)
(2)
Подберем вспомогательное неизвестное 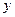 так, чтобы правая часть (2) превратилась в полный квадрат. Что возможно при условии, что
так, чтобы правая часть (2) превратилась в полный квадрат. Что возможно при условии, что 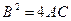 , где
, где 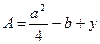 ,
, 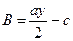 ,
, 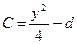 . Если
. Если 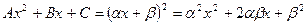 , сравнивая коэффициенты при
, сравнивая коэффициенты при 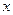 :
: 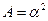 ,
, 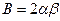 ,
, 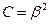 , откуда
, откуда 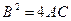 . Обратно, если
. Обратно, если 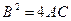 , то
, то 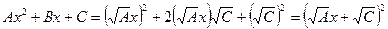 .
.
Подставляя в равенство 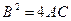 выражения
выражения  А, В,С, находим, что
А, В,С, находим, что 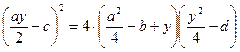 .
.
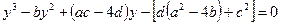 (3)
(3)
(3)- кубическая резольвента.
Пусть 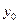 - какой-нибудь корень уравнения (3). Подставляя
- какой-нибудь корень уравнения (3). Подставляя 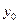 в (2) в правой части получим полный квадрат:
в (2) в правой части получим полный квадрат:
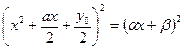
Откуда 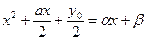
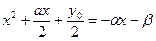
Эти два квадратных уравнения дадут все четыре корня уравнения (1). Итак, решение уравнения четвертой степени сводится к решению одного уравнения третьей степени и двух уравнений второй степени, и так же решается в радикалах. При нахождении корней уравнения типа (1) по способу Феррари проводят последовательно все преобразования, не запоминая кубическую резольвенту.
Пример. 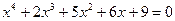
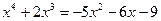
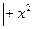
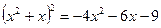
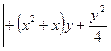
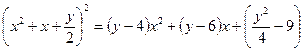
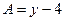 ,
, 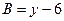 ,
, 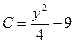
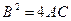
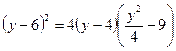
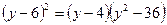
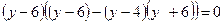
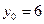
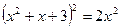
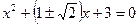
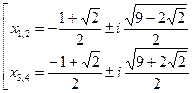
II способ Левая часть уравнения 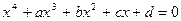 раскладывается на два множителя второй степени, которые последовательно приравниваются к нулю. Для нахождения такого разложения левую часть представляют как разность квадратов, для чего сначала представляют ее как разность между квадратом некоторого квадратного трехчлена и многочленом второй степени:
раскладывается на два множителя второй степени, которые последовательно приравниваются к нулю. Для нахождения такого разложения левую часть представляют как разность квадратов, для чего сначала представляют ее как разность между квадратом некоторого квадратного трехчлена и многочленом второй степени: 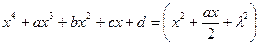 - (члены степени не больше двух), оставляя
- (члены степени не больше двух), оставляя 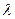 пока неопределенным. В вычитаемое при этом входят лишние члены уменьшаемого(члены степени не больше 2) и такие же члены левой части (с обратным знаком). Для того, чтобы вычитаемое было полным квадратом, надо, чтобы его дискриминант был равен нулю. Это условие дает уравнение третьей степени относительно
пока неопределенным. В вычитаемое при этом входят лишние члены уменьшаемого(члены степени не больше 2) и такие же члены левой части (с обратным знаком). Для того, чтобы вычитаемое было полным квадратом, надо, чтобы его дискриминант был равен нулю. Это условие дает уравнение третьей степени относительно 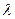 . Беря в качестве
. Беря в качестве 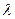 любой корень этого уравнения, получаем искомое.
любой корень этого уравнения, получаем искомое.
Пример.
1) 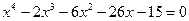
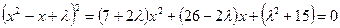
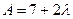 ,
, 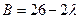 ,
, 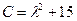 ,
,
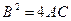
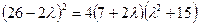
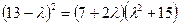
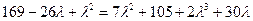
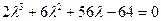
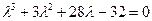
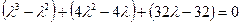
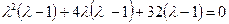
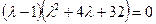
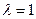
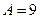 ,
, 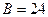 ,
, 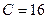
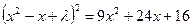
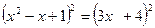
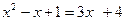
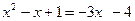
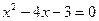
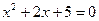
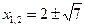
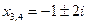
*2) 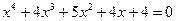
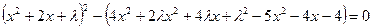
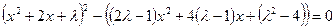
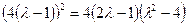
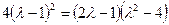
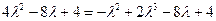
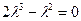
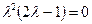
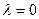
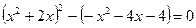
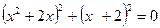
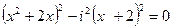
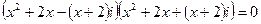
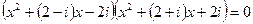
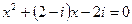
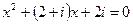
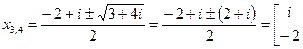
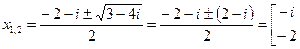
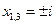
 2015-05-25
2015-05-25 5495
5495