§6. Поле комплексных чисел.
Мнимая единица. Алгебраическая и тригонометрическая формы записи комплексного числа. Равенство комплексных чисел. Арифметические операции над комплексными числами и их геометрическая интерпретация. Комплексная плоскость и формула Муавра. Извлечение корня из комплексного числа. Двучленные уравнения.
Поле комплексных чисел С – это расширение поля действительных чисел, полученное присоединением корня i (мнимая единица), квадратного уравнения x 2+1=0. Элементы поля С называют комплексными числами. Причём,
С={a|a= a+bi, a ÎR, b ÎR}
Представление комплексного числа a в виде a+b i единственно, т.е.
a+bi = с+di Û(a=c и b=d),
a= a+bi – алгебраическая форма записи комплексного числа. Действительные числа a,b называются соответственно действительной частью и коэффициентом при мнимой части числа a. Во множестве комплексных чисел определена операция сопряжения, однозначно сопоставляющая каждому числу a= a+bi сопряжённое с ним число 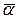 = a–bi.
= a–bi.
Простейшие свойства операции сопряжения:
1) 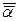 =a; 2)
=a; 2) 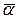 =aÛaÎR; 3)
=aÛaÎR; 3) 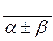 =
= 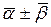 ; 4)
; 4) 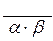 =
= 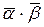 ;
;
5) 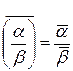 , при b¹0; 6) (a+
, при b¹0; 6) (a+ 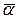 )ÎR; 7) a.
)ÎR; 7) a. 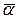 ÎR 8) если a¹0, то
ÎR 8) если a¹0, то 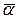 .a>0.
.a>0.
Операции сложения, вычитания, умножения и деления комплексных чисел a= a+bi и b= с+di определяются правилами:
a+b=(a+bi)+(с+di)=(a+c) + (b+d) i;
a – b=(a+bi) – (с+di)=(a–c) + (b–d) i;
a.b=(a+bi).(с+di)=(ac–bd)+(ad+bc) i;
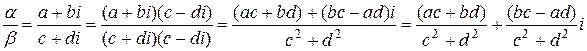
(деление определено, если b¹0).
 Каждое комплексное число a= a+bi определяет пару (a,b) действительных чисел, которой на координатной плоскости соответствует точка М с координатами (a,b) или радиус-вектор
Каждое комплексное число a= a+bi определяет пару (a,b) действительных чисел, которой на координатной плоскости соответствует точка М с координатами (a,b) или радиус-вектор 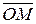 . Указанные соответствия взаимно однозначны. Этот факт позволяет представлять числа как точки координатной плоскости, или как радиус-векторы. Сложение, вычитание комплексных чисел можно представить как сложение (вычитание) соответствующих векторов.
. Указанные соответствия взаимно однозначны. Этот факт позволяет представлять числа как точки координатной плоскости, или как радиус-векторы. Сложение, вычитание комплексных чисел можно представить как сложение (вычитание) соответствующих векторов.
На плоскости можно использовать не только декартову xOy, но и полярную систему координат Ox (рис.1), в которой a= r.cosj, b=r.s i nj, тогда a= a+bi = r.(cosj+ i .s i nj).
Запись числа a в виде r.(cosj+ i .s i nj) называется тригонометрической формой комплексного числа. Длина вектора 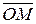 , изображающего число a= a+bi, называется модулем этого комплексного числа:
, изображающего число a= a+bi, называется модулем этого комплексного числа:
r=½a½= 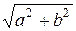
Угол, который образует вектор 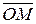 , с положительным направлением оси Ox, называется аргументом комплексного числа a¹0:
, с положительным направлением оси Ox, называется аргументом комплексного числа a¹0:
arga=j,
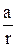 =cosj,
=cosj, 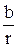 =s i nj.
=s i nj.
Полярные координаты точки, в отличие от декартовых, определяются неоднозначно: если r1.(cosj1+ i .s i nj1)= r2.(cosj2+ i .s i nj2), то r1=r2 и j1=j2+2pk, где kÎZ.
В тригонометрической форме над комплексными числами удобно выполнять действия умножения, деления, возведения в степень и извлечения корней натуральной степени: если a1=r1.(cosj1+ i .s i nj1), a2=r2.(cosj2+ i .s i nj2), то
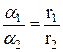 (cos(j1 – j2)+ i .s i n(j1 – j2));
(cos(j1 – j2)+ i .s i n(j1 – j2));
a1.a2=r1.r2(cos(j1+j2)+ i .s i n(j1+j2));
(a)n=rn(cos(nj)+ i .s i n(nj));
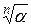 =r.(cosg+ i .s i ng), где r=
=r.(cosg+ i .s i ng), где r= 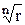 , a=
, a= 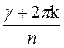 , k=0..(n – 1).
, k=0..(n – 1).
При умножении комплексных чисел их модули перемножаются, а аргументы складываются, поэтому умножение на комплексное число b с модулем, равным 1, геометрически можно интерпретировать как поворот на угол arg b вокруг начала координат, т.е. соответствие a®ba (или функция f= ba) при | b |=1 задаёт преобразование комплексной плоскости, именно указанный поворот.
Параллельный перенос на вектор, определяемый комплексным числом g, описывается функцией f= ba+g. Умножение числа a на комплексное число b сводится к растяжению вектора, изображающего a, в |b| раз и повороту на угол j=arg b вокруг начала координат. Функция f= ba+g, a,b Î С, b ¹1, задаёт на комплексной плоскости гомотетию с центром в точке g /(1 –b), коэффициентом k=| b | и поворот с этим центром на угол j=arg b, что следует из равенства:
ba+g=b (a– g/(1 –b))+g/(1 –b);
При извлечении корня n-ной степени из числа a все его n значений имеют одинаковые модули, а аргументы различаются на углы, кратные 2p/n. Таким образом, все значения 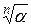 располагаются на окружности радиусом
располагаются на окружности радиусом 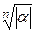 с центром в начале координат через угол 2p/n.
с центром в начале координат через угол 2p/n.
Множество всех корней n-ой степени из числа a можно получить умножением одного из этих корней на все значения 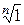 .
.
Используя формулу Эйлера
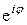 =cosj+ i .s i nj,
=cosj+ i .s i nj,
всякое комплексное число можно представить в виде:
a=|a| 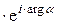
 2015-05-25
2015-05-25 1567
1567
