Пример 6. Пусть в одном из трех ящиков находится 3 белых и 2 черных шара, во втором – 2 белых и 3 черных, в третьем – только белые шары. Из наугад
выбранного ящика извлекают один шар. Найти вероятность того, что он белого цвета.
Обозначим через А событие, состоящее в том, что выбранный шар белого цвета. Вероятность этого события зависит от того, из какого ящика выбран шар.
Рассмотрим события:
H 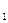 - шар взят из первого ящика,
- шар взят из первого ящика,
H 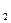 - шар взят из второго ящика,
- шар взят из второго ящика,
H 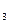 - шар взят из третьего ящика.
- шар взят из третьего ящика.
События H 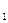 , H
, H 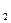 , H
, H 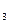 - несовместны, тогда событие А можно представить в виде суммы произведений
- несовместны, тогда событие А можно представить в виде суммы произведений
А= H 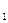 А + H
А + H 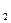 А + H
А + H 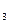 А
А
Применяя формулы сложения и умножения получим,
Р(А) = Р(H 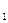 А + H
А + H 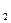 А + H
А + H 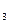 А) = Р(H
А) = Р(H 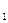 А) + Р(H
А) + Р(H 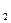 А) + (H
А) + (H 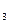 А) =
А) =
Р(H 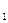 )Р(А/ H
)Р(А/ H 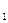 ) + Р(H
) + Р(H 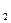 )Р(А/ H
)Р(А/ H 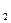 ) + Р(H
) + Р(H 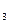 )Р(А/ H
)Р(А/ H  ) =
) = 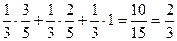
Это и есть формула полной вероятности. Запишем ее в общем виде.
Пусть событие А может произойти только совместо с одним из событий
H  , H
, H  , …, H
, …, H 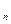 , образующих полную группу несовместных событий (гипотез).
, образующих полную группу несовместных событий (гипотез).
Вероятность Р(А) определяется формулой полной вероятности
Р(А) = 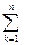 Р(H
Р(H 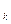 )P(A/ H
)P(A/ H 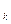 ),
),
где 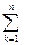 Р(H
Р(H 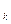 ) = 1.
) = 1.
Пример 7. На двух автоматических станках изготовляются одинаковые валики. Вероятность изготовления валика высшего сорта на первом станке равна 0,95, а на втором - 0,80. Изготовленные на обоих станках нерассортированные валики находятся на складе, среди них валиков, изготовленных на первом станке, в три раза больше, чем на втором. Определить вероятность того, что наудачу взятый валик окажется высшего сорта.
Обозначим А - событие, состоящее в том, что взятый наудачу валик окажется
высшего сорта;
В 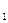 - событие, состоящее в том, что взятый наудачу валик
- событие, состоящее в том, что взятый наудачу валик
произведен на первом станке;
В 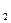 - событие, состоящее в том, что валик произведен на втором
- событие, состоящее в том, что валик произведен на втором
станке.
Применив формулу полной вероятности получим:
Р(А) = Р(В 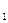 )Р(А/ В
)Р(А/ В 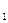 ) + Р(В
) + Р(В 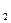 )Р(А/ В
)Р(А/ В 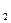 ).
).
Поскольку валиков, произведенных на первом станке, в 3 раза больше, чем на втором, то Р(В 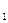 ) =
) = 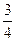 , Р(В
, Р(В 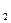 ) =
) = 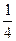 .
.
В задаче даны условные вероятности:
Р(А/ В 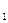 ) = 0,92, Р(А/ В
) = 0,92, Р(А/ В 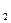 ) = 0,80.
) = 0,80.
Искомая вероятность
Р(А) = 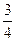
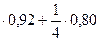 = 0,89.
= 0,89.
Формулы Байеса.
В условиях Примера 6, выбранный из ящика шар, оказался белого цвета. Найти вероятность того, что шар был взят из третьего ящика.
Эта задача отличается тем, что известно событие, наступившее в результате эксперимента: А – извлечен шар белого цвета. Требуется найти вероятность гипотезы при условии, что наступило событие А, т.е. Р(Н 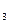 /А).
/А).
Рассмотрим вероятность Р(А Н 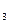 ), по формуле умножения
), по формуле умножения
Р(А Н 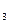 ) = Р(А)Р(Н
) = Р(А)Р(Н 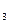 /А) = Р(Н
/А) = Р(Н 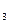 )Р(А/ Н
)Р(А/ Н 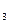 ).
).
Из последнего равенства выразим искомую вероятность
Р(Н 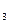 /А) =
/А) = 
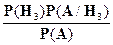
 ,
,
где Р(А) – полная вероятность события А.
Полученное равенство и есть формула Байеса для Н 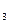 . Аналогично можно получить формулы для гипотез H
. Аналогично можно получить формулы для гипотез H 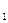 и H
и H 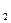 .
.
Используя результаты Примера 6, получим
Р(Н 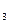 /А) =
/А) = 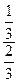 =
= 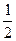 .
.
Запишем формулы Байеса в общем виде:
Р(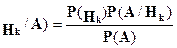 , Р(А) – полная вероятность события А,
, Р(А) – полная вероятность события А,
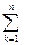 Р(H
Р(H 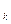 ) = 1, k =
) = 1, k = 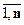 .
.
Пример 8. В условиях Примера 7, взятый наугад валик оказался высшего сорта.
Определить вероятность того, что он произведен на первом станке.
Используя обозначения Примера 7, по формуле Баейса получим:
Р(В 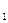 /А) =
/А) = 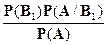 =
= 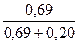 = 0,76.
= 0,76.
 2015-06-10
2015-06-10 1318
1318
