Математическим фундаментом теории надежности являются
· теория вероятностей
· случайные процессы,
· комбинаторика
· математическая статистика
· алгебра логики
Поэтому данная лекция будет посвящена обзору основных понятий и соотношений теории вероятностей. Приводимые сведения будут носить обзорный характер и ни в коем случае не могут подменить изучение теории вероятностей в соответствующих математических курсах.
I. Случайные события. Основные формулы теории вероятностей.
Будем называть опытом осуществление определенных условий и действий, при которых наблюдается изучаемое случайное явление. Любая качественная характеристика результата опыта есть событие. События можно разделить на три вида – достоверные, невозможные, случайные.
· достоверное событие - событие, обязательно происходящее в результате опыта
· невозможное событие - событие, заведомо не происходящее в результате опыта
· случайное событие - событие, которое либо происходит, либо не происходит в результате опыта
Случайные события могут быть совместными и несовместными.
События называются совместными, если появление одного из них не исключает появление других событий
События называются несовместными, если появление одного из них исключает появление других событий
Случайные события бывают зависимые и независимые.
Независимые события - появление одного из них не влияет на появление других
Зависимые события - появление одного из них влияет на появление других
Противоположное (дополнительное) событие относительно случайного события А есть событие`А, состоящее в непоявлении А.
Полная группа событий – такая совокупность событий, что в результате опыта обязательно должно произойти хотя бы одно из событий этой совокупности.
Рассмотрим последовательность n одинаковых опытов, в результате каждого из которых появляется или не появляется событие A. Естественной характеристикой события А в этой последовательности опытов является частотаего появления:
W(A)=m/n, (1)
где m – число появления событий А, n – общее число опытов.
Очевидно, что частота любого события представляет собой правильную дробь или равна нулю или единице.
Основной теоретической характеристикой случайного события A является его вероятность P(А). В современной теории вероятностей вероятность случайного события А вводится аксиоматически. Но с прикладной точки зрения вероятностью события называется число, характеризующее частоту события при большом числе опытов (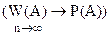 .
.
Наиболее часто изучаемые в теории надежности случайные события – есть события отказов технических объектов.
Теоремы Сложения Вероятностей.
Сумма событий А и В – это событие (А+В), состоящее в появлении событий А, В, или их обоих (АВ). Для трех событий: (А+В+С) – А, В, С, АВ, АС, ВС, АВС.
• Если А и В – несовместны, то
Р(А+В) = Р(А) + Р(В) (2)
В самом деле, если в результате n опытов появилось m раз событие A и l раз событие B, то интересующее нас сложное событие (A+B) появилось m+l раз и его частота согласно (1) равна (m+l)/n.
• Если А и В – совместны, то
Р(А+В) = Р(А) + Р(В) - P(AB) (3)
Для иллюстрации на рис.1. показана сумма двух событий A и B как область, объединенная жирной чертой. a) соответствует случаю, когда A и B совместны, b) – несовместны.
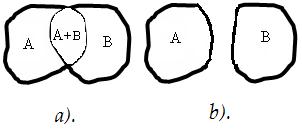
Рис.1. Объединение событий A и B.
• Если А, В, C – совместны, то
Р(А+В+С) = Р(А)+Р(В)+P(C)-Р(АВ)-Р(АC)-Р(ВC)+P(ABC) (4)
• Если А, В, С, … - полная группа несовместных событий, то
Р(А) + Р(В) + Р(С) + …. = 1 (5)
• Для противоположных событий:
Р (А) + Р (`А) = 1 (6)
Теоремы Умножения Вероятностей
Произведение событий А, В, С… – это событие, состоящее в совместном появлении событий (АВС…)
• Если А и В – независимы, то
Р(АВ) = Р(А)*Р(В) (7)
• Если А и В – зависимы, то
Р(АВ) = Р(А)*Р(В/A) = Р(В)*Р(А/В), (8)
где Р(В/A) – условная вероятность появления события B при условии, что событие А произошло
Пусть B1,B2,…Bn – полная группа несовместных событий. Случайное событие А наступает при наступление одного из В. Тогда вероятность появления события A равна
P(A)=P(B1)P(A/B1)+ P(B2)P(A/B2) +…+ P(Bn)P(A/Bn) (9)
Поток Событий.
Потоком событий называют последовательность событий, происходящих в случайные моменты времени. Примером потока событий является последовательность отказов технической системы.
Если поток обладает свойствами стационарности, отсутствия последействия и ординарности, то это простейший или пуассоновский поток. Пуассоновский поток событий (отказов) характеризуется интенсивностью λ, т.е. средним числом событий, которые появляются в единицу времени. При известной постоянной интенсивности потока вероятность появления k событий за время Dt для простейшего потока определяется формулой Пуассона:
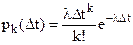 (10)
(10)
Эта формула отражает все свойства простейшего потока.
Стационарность – вероятностные характеристики потока на интервале времени зависят только от протяженности интервала, но не зависят от момента его начала.
Ординарность - в бесконечно малом интервале времени вероятность появления более чем одного события стремиться к нулю
Отсутствие последействия – вероятность появления события в потоке не зависит от всей предшествующей реализации потока
II. Законы распределения и числовые характеристики случайных величин
Если мы будем рассматривать пусть даже однотипные технические устройства и зададимся целью точно определить какие-либо их надежностные характеристики, например, время работы до отказа, время восстановления после отказа, величину износа за определенный срок и пр., то сделать это мы не сможем. Эти величины случайны. Поэтому для теории и практики надежности необходимо научится оперировать со случайными величинами.
Случайной называют величину, которая в результате опыта принимает одно заранее неизвестное значение, а в результате разных опытов может принимать различные значения. По аналогии с интерпретацией случайного события, как качественной характеристикой опыта, можно сказать, что случайная величина является количественной характеристикой опыта. Чтобы охарактеризовать случайную величину необходимо указать множество ее возможных значений и вероятности этих значений. Случайные величины могут быть дискретными и непрерывными.
Дискретная случайная величина может принимать только конечное или счетное множество значений. Например, число отказов объекта за заданный интервал времени есть дискретная случайная величина. Чтобы охарактеризовать дискретную случайную величину нужно перечислить ее возможные значения и указать вероятности того, что она примет эти значения. Законом распределения дискретной случайной величины называют соответствие между ее возможными значениями и их вероятностями. Закон распределения может быть задан таблично, графически, аналитически. При табличном задании первая строка содержит возможные значения случайной величины X, а вторая их вероятности:
Таблица 1. Ряд распределения дискретной случайной величины X.
| X | x1 | x2 | x3 | … | xn |
| P | p1 | p2 | p3 | … | pn |
Часто такую таблицу называют рядом распределения случайной величины X.
Графическая интерпретация ряда распределения называется многоугольником распределения:
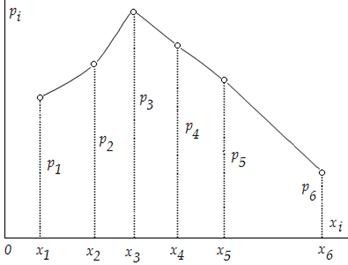
Рис.2. Многоугольник распределения дискретной случайной величины.
Очевидно, что 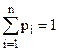 , так как в результате опыта дискретная случайная величина обязательно примет одно из перечисленных значений.
, так как в результате опыта дискретная случайная величина обязательно примет одно из перечисленных значений.
Примером аналитического задания закона распределения может служить формула Бернулли, определяющая вероятность того, что в серии n независимых опытов, в каждом из которых событие A появляется с вероятностью p (q=1-p), событие А появится ровно k раз:
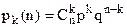 (11)
(11)
Совокупность вероятностей (11) называют биномиальным распределением.
Наиболее полно случайная величина характеризуется законом распределения, однако для теории вероятностей и ее применений (в том числе теории надежности) большую роль играют некоторые агрегированные количественные характеристики, описывающие случайную величину в целом и получаемые по определенным правилам на основе знания распределений. Особое значение среди числовых характеристик имеют математическое ожидание (среднее) и дисперсия.
Математическое ожидание M[X] дискретной случайной величины X, принимающей значение x1, x2, …xn c вероятностями p1, p2, … pn (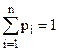 ), определяется суммой произведений ее возможных значений на их вероятности:
), определяется суммой произведений ее возможных значений на их вероятности:
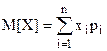 (12)
(12)
Свойства математического ожидания:
· математическое ожидание постоянной величины равно ей самой: M[c] = c
· постоянный множитель можно выносить за знак математического ожидания:M[cX] = cM[X]
· математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M[XY] = M[X] M[Y]
· математическое ожидание суммы (разности) двух случайных величин равно сумме (разности) их математических ожиданий: M[X±Y] = M[X] ± M[Y]
· математическое ожидание числа появлений события A в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании: np
Для оценки разброса значений случайной величины около ее среднего значения используется несколько числовых характеристик, важнейшей из которых является дисперсия. Дисперсия определяется как квадрат уклонения случайной величины от ее математического ожидания:
D[X] = M(X-M[X])2 (13)
Свойства дисперсии:
· дисперсия постоянной величины равна нулю: D[c] = 0
· постоянный множитель выносится за знак дисперсии и возводится в квадрат: D[cX] = c2D[X]
· дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины: D[c+X] = D[X]
· дисперсия суммы (разности) двух независимых случайных величин равна сумме (разности) дисперсий D[X±Y]=D[X] ± D[Y]
· дисперсия числа появлений события A в n независимых испытаниях равна: npq.
Числовая характеристика, также определяющая разброс относительно математического ожидания, но имеющая размерность случайной величины, называется средним квадратическим отклонением
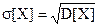 (14)
(14)
Примером непрерывной случайной величины является время безотказной работы объекта, время его ремонта после отказа, время выполнения логистических операций, связанных с ремонтами, техническими осмотрами и профилактическим обслуживанием. Непрерывная случайная величина имеет несчетное множество возможных значений, поэтому описать ее перечислением этих значений и заданием их вероятностей, как в дискретном случае, не представляется возможным. Для описания непрерывной случайной величины было введено понятие функции распределения. Функцией распределения F(x) непрерывной случайной величины X называется вероятность того, что X примет значение меньшее, чем х:
F(x)=p(X<x) (15)
Иногда (5) называют интегральной функцией распределения.
Функция распределения обладает следующими свойствами
1. Значения F(x) принадлежат отрезку (0,1): 0£ F(x) £1.
2. F(x) – неубывающая функция: если x2 > x1, то F(x2) > F(x1).
3. Если возможные значения непрерывной случайной величины принадлежат отрезку (a,b), то F(x)=0 при x<a и F(x)=1 при x³b.
4. Если возможные значения случайной величины размещены на всей прямой (-¥,¥), то справедливы граничные соотношения: limx®-¥ F(x)=0; limx®¥ F(x)=1.
Вероятность того, что случайная величина X примет значение из интервала (a,b), равна приросту функции распределения на этом интервале: p(a £ X < b) = F(b)-F(a). Соотношение легко выводится, если мы определим три случайных события A, B и С таких, что A: X<b; B: X < a; C: a £ X < b. Тогда A=B+C и при несовместности событий B и C получаем P(X<b)=P(X<a)+P(a £ X < b).
И как следствие -.вероятность того, что непрерывная случайная величина примет единственное (конкретное) значение, равна нулю.
Исследование функции распределения не дает ответа на вопросы как определить является ли данное число х возможным значением случайной величины, и можно ли определить, какие ее значения более вероятны и какие менее вероятны? Чтобы ответить на этот вопрос рассмотрим бесконечно малый интервал числовой оси Dx. Тогда вероятность того, что случайная величина X примет значение, заключенное между x и x+Dx, может служить практической мерой возможности данного значения x. При этом разумно соотнести это значение с величиной интервала Dx. Таким образом, вводится понятие плотности вероятности f(x):
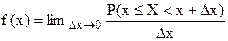 (16)
(16)
Если плотность вероятности случайной величины X в точке х отлична от нуля, то х является ее возможным значением. Если плотность вероятности в точке х1 больше, чем в х2, то значение х1 непрерывной случайной величины Х более вероятно, чем х2.
Учитывая свойства функции распределения, (16) можно записать как
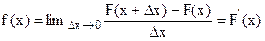 (17)
(17)
То есть плотность вероятности есть первая производная от интегральной функции распределения. Иногда плотность вероятности называют дифференциальной функцией распределения.
Учитывая соотношение 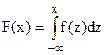 , нетрудно показать, что вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равна
, нетрудно показать, что вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a,b), равна
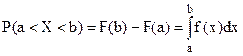 (18)
(18)
Отметим два важных свойства плотности вероятности:
1. плотность вероятности неотрицательная функция: f(x)³0
2. 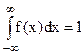
Числовые характеристики непрерывной случайной величины выражаются следующим образом
· математическое ожидание

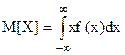 (19)
(19)
· дисперсия
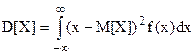 (20)
(20)
III. Законы распределения непрерывных случайных величин (СВ), наиболее часто используемые в теории надежности
Плотность вероятности нормально распределенной случайной величины X выражается формулой
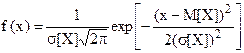 (21)
(21)
Нормальный закон распределения имеет широкое практическое значение. Это объясняется тем, что если случайная величина является суммой большого числа малых слагаемых, то закон распределения этой величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. В большинстве практических случаев случайная величина формируется под воздействием многих противоположно действующих факторов, что и определяет широкую применимость этого закона. Нормальный закон является предельным, а именно, при определенных условиях многие законы распределения приближаются к нормальному. Классическим примером нормально распределенной случайной величины являются ошибки измерений. В теории надежности нормальный закон часто применяется для адекватного моделирования времен восстановления работоспособности отказавшего объекта.
Два параметра нормального закона имеют смысл математического ожидания M[X] и среднего квадратического отклонения s[Х] случайной величины X. На рис.3. представлено семейство кривых, изображающих плотность нормального распределения. Эти кривые симметричны относительного первого параметра (математического ожидания). Поэтому первый параметр еще называют центром симметрии (рассеивания) распределения. Ордината кривой нормальной плотности при х=M[X] равна 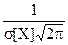 . При уменьшении второго параметра (среднего квадратического отклонения) эта ордината неограниченно возрастает. При этом кривая пропорционально сплющивается вдоль оси абсцисс, так что ее площадь остается равной единице. Очевидно, что при уменьшении дисперсии плотность вероятности в области центра рассеивания начинает возрастать, а в остальных точках убывать.
. При уменьшении второго параметра (среднего квадратического отклонения) эта ордината неограниченно возрастает. При этом кривая пропорционально сплющивается вдоль оси абсцисс, так что ее площадь остается равной единице. Очевидно, что при уменьшении дисперсии плотность вероятности в области центра рассеивания начинает возрастать, а в остальных точках убывать.
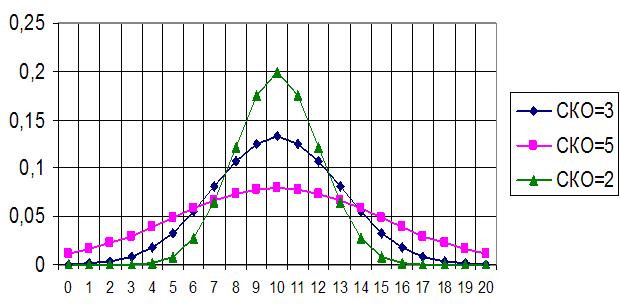
Рис. 3. Плотность вероятности нормального распределения.
При M[X]=0 и s[Х ]=1 имеем нормированное нормальное распределение:
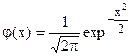 (22)
(22)
Очевидно 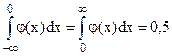 .
.
Определим вероятность того, что случайная нормально распределенная величина T (например, время работы до отказа) принадлежит интервалу (t1,t2): 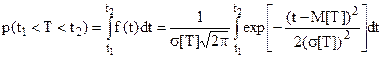 . Обозначим
. Обозначим 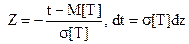 и введем новые пределы интегрирования
и введем новые пределы интегрирования 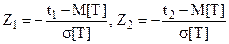 . В результате введения z от f(t) переходим к нормированной функции j(z). Тогда
. В результате введения z от f(t) переходим к нормированной функции j(z). Тогда 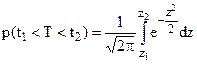 .
.
Выражение 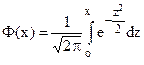 называется функцией Лапласа. Значения этой функции в зависимости от x приведены в специальных таблицах, поэтому
называется функцией Лапласа. Значения этой функции в зависимости от x приведены в специальных таблицах, поэтому
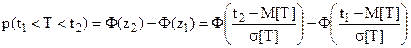 (23)
(23)
Пример. T– нормально распределенное время работы объекта до отказа с M[T]=300ч. и s[T]=50ч.. Необходимо определить вероятность того, что объект откажет на интервале времени (200ч., 400ч.): P(200<t<400)= Ф((400-300)/50)-Ф((200-300)/50)=2Ф(2)=2*0,4772=0,9544.
Для нормального распределения действует так называемое “правило трех сигм”. Вероятность того, что отклонение случайной величины от математического ожидания не выйдет за пределы утроенного среднего квадратического отклонения, равна 0,9973. В самом деле
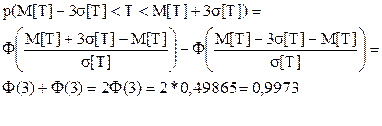 (24)
(24)
Правило (24) позволяет с достаточной для практики точностью указать интервал возможных значений нормально распределенной случайной величины.
2. Усеченное нормальное распределение
Усеченное нормальное распределение получается из нормального при ограничении интервала возможных значений случайной величины (рис.4). Например, случайные времена работы до отказа и восстановления могут принимать только положительные значения.
Плотность вероятности усеченного распределения 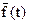 задается с помощью специального нормирующего множителя (
задается с помощью специального нормирующего множителя (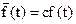 ), определяемого из условия, что площадь под кривой
), определяемого из условия, что площадь под кривой 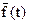 на интервале (t1,t2) равна единице
на интервале (t1,t2) равна единице
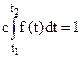 (25)
(25)
Нормирующий множитель можно определить, пользуясь функциями Лапласа
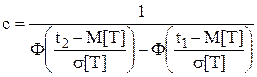 (26)
(26)
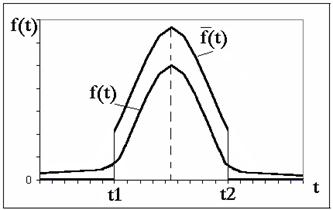
Рис.4. Плотность вероятности усеченного нормального распределения.
Для случайных времен работы до отказа имеем
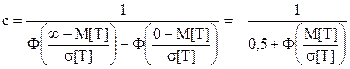 (27)
(27)
3. Показательное распределение.
Показательное (экспоненциальное) распределение играет исключительную роль в теории надежности и практике расчетов. Оно достаточно точно описывает “надежностной поведение” объектов на стационарных участках функционирования, когда период приработки уже завершен, а период старения еще не начался.
Экспоненциальная функция распределения имеет вид
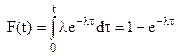 (28)
(28)
Плотность экспоненциального распределения (рис.5) есть
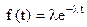 , (29)
, (29)
где λ – параметр распределения.
Числовые характеристики экспоненциального распределения определяются через параметр λ:
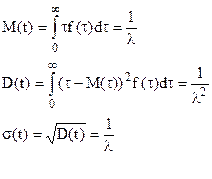 (30)
(30)
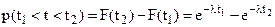 (31)
(31)
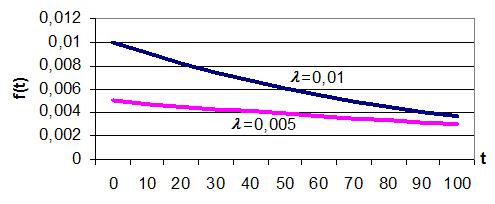
Рис.5. Плотность вероятности экспоненциального распределения.
Рассмотрение кривой плотности (рис.5) позволяет сделать вывод о том, что значения случайных времен отказа объекта, подчиненных экспоненциальному закону, практически равновероятны на всем реальном сроке его использования. Вероятность того, что объект безотказно проработает время больше или равное математическому ожиданию, мала, а именно
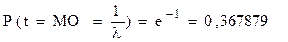 (32)
(32)
Экспоненциальное распределение является наиболее популярным для моделирования случайных времен отказа элементов систем. Достаточно сказать, что все стандарты по расчету надежности элементной базы, как отечественные, так и зарубежные, основываются на показательном распределении. Это объясняется следующим:
· удобством сбора статистики (только один параметр распределения)
· практически все аналитические модели надежности восстанавливаемых систем, работают при допущении об экспоненциальном характере времен отказа и восстановления
· в современных теоретических работах показано, что предположение об “экспоненциальности” элементов позволяет (в ряде случаев) получать нижние оценки показателей надежности системы в целом
· при экспоненциальных распределениях случайных времён до отказа и восстановления значительно упрощаются аналитические выражения для показателей надежности элементов и систем.
4. Распределение Вейбулла-Гнеденко
Вейбулл предложил это распределение для описания статистических данных по усталостной прочности стали. Функция распределения и плотность вероятности для закона Вейбулла имеют вид:
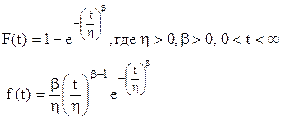 , (33)
, (33)
где β - параметр формы, η – параметр масштаба, оба параметра положительные (см. рис.6)
Если β =1 – имеем показательное распределение с математическим ожиданием равным h. Если β < 1 (математическое ожидание > h) то имеем “молодеющее” распределение, т.е. вероятность отказа со временем уменьшается и распределение подходит для моделирования периодов приработки технических объектов. При β > 1 (математическое ожидание < h) – “стареющее” распределение. Таким образом, это распределение можно применять на всех этапах жизни технических объектов, что и определяет популярность распределения Вейбулла при моделировании надежности.
При обработке статистики отказов технических объектов по значению параметра β можно дать рекомендации по их замене:
• 1 < b < 4 – так называемое медленное старение (можно ремонтировать, а не заменять)
• b > 4 – быстрое старение (оборудование надо заменять)
В западной литературе направление математической статистики, связанное с обработкой данных об отказах, называется вейбулловским анализом.
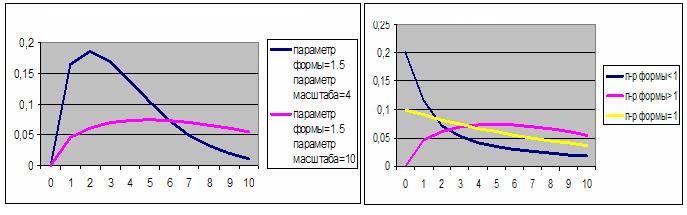
Рис.6. Кривые плотности распределения Вейбулла
5. Гамма-распределение
Плотность вероятности гамма-распределения имеет выражение
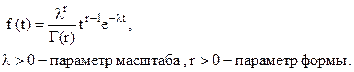 (34)
(34)
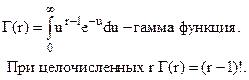
При целых r>1 имеем распределение Эрланга, впервые применившего его для решения задач массового обслуживания. Плотность этого распределения и числовые характеристики выражаются следующими формулами:
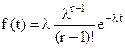 (35)
(35)
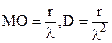 (36)
(36)
Распределение Эрланга описывает распределение суммы r независимых случайных величин, каждая из которых подчиняется экспоненциальному закону. Этот факт позволяет использовать распределение при решении многих задач анализа надежности. Приведем пример использования распределения Эрланга для расчета среднего времени работы до отказа резервированной системы. Система состоит из трех “’экспоненциально распределенных”элементов (рис.7). Первый элемент – рабочий. Остальные резервные, последовательно замещающие рабочий элемент при его отказе. Резервные элементы находятся в ненагруженном резерве (не работают), и не могут отказывать, вплоть до включения. Значение параметра l=0,001 1/ч.
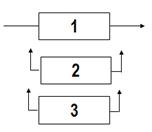
Рис.7. Система с динамическим резервированием.
r=3, следовательно, согласно (36) среднее время равноr/l=3000ч
При больших r гамма-распределение сходится к нормальному с параметрами M[T]норм=rМ[T] и D[T]норм=rD[T].
Литература к лекции 2.
1. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности. – М.: Наука, 1965.
2. Пугачев В.С. Введение в теорию вероятностей. М.: Наука, 1968.
3. Вентцель Е.С. Теория вероятностей. М.: Наука, 1969.
4. Кондратенков В.А., Котельников Г.Н., Мамченков В.Л. и др. Вопросы теории надежности технических систем. Смоленск, РУСИЧ, 1998.
5. Гнеденко Б.В. Курс теории вероятностей (7 издание). - М.: УРСС, 2001.
Лекция 3. Основные показатели надежности технических объектов
Показатель надежности – техническая характеристика, количественным образом определяющая одно или несколько свойств, составляющих надежность объекта. Показатель надежности количественно характеризует, в какой степени данному объекту или данной группе объектов присущи определенные свойства, обуславливающие надежность. Показатели надежности могут иметь размерность или быть безразмерными. Исследуемые в рамках теории надежности объекты можно разделить на два больших класса – восстанавливаемые и невосстанавливаемые. Следует иметь ввиду, что эти понятия относительные и зависят от выполняемых объектом функций и режимов работы. Одно и то же изделие - компьютер может рассматриваться как невосстанавливаемый объект, если он используется в системе управления ракеты, летящей на марс, или как восстанавливаемый объект, если он работает в локальном режиме и используется для проведения бухгалтерских расчетов. Под восстановлением объекта понимается не только ремонт той или иной его части, но и их замена, а возможно, и полная замена всего объекта.
Показатели надежности также можно разделить на два класса – показатели надежности невосстанавливаемых и восстанавливаемых объектов.
Для показателей надежности существуют две формы представления: вероятностная и статистическая. Вероятностная форма обычно бывает удобнее при априорных аналитических расчетах надежности. Статистическая – при экспериментальном исследовании надежности технических объектов.
Важным понятием, присутствующим во многих формулировках показателей надежности, является наработка. Наработка это продолжительность или объем работы объекта, т.е. наработка может измеряться не только в единицах времени, но и единицах выработки продукции, пройденном расстоянии и пр. Например, в одном из зарубежных стандартов по расчету надежности устройств военно-морской техники частотные показатели имеют размерность 1/милю.
Отказы объекта обычно разделяют на внезапные и постепенные.
Внезапный отказ – отказ, характеризующийся скачкообразным изменением значений одного или нескольких основных параметров объекта.
Постепенный отказ – отказ, характеризующийся постепенным изменением значений одного или нескольких основных параметров объекта.
Внезапный отказ обычно является следствием постепенного накопления неисправностей и повреждений и его внезапность обуславливается отсутствием наблюдений за этим накоплением.
Будем использовать следующие обозначения:
ξ1 – случайная наработка объекта до первого отказа.
ξ1(i) – реализация случайной величины ξ1 для i-го объекта.
F1(t) = P(ξ1<t) – распределение времени до первого отказа
n(t) – число отказавших объектов к моменту времени t.
N(t) – число работоспособных объектов к моменту времени t.
Dn(t,t¢) – число объектов, отказавших на интервале времени (t,t¢).
I. Показатели надежности невосстанавливаемых объектов
Будем приводить вероятностную и статистическую формы представления показателей. Статистические показатели будем обозначать как и вероятностные но с “крышечкой” cверху. При статистическом представлении будем рассматривать схему, когда несколько объектов работают до отказа. В этом случае статистические показатели имеют простое частотное толкование и с ростом числа испытываемых объектов будут сходится в пределе к аналогичным вероятностным показателям.
1. Вероятность безотказной работы объекта на интервале времени от 0 до t
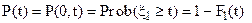 . (1)
. (1)
Вероятность безотказной работы определяется как вероятность того, что объект проработает безотказно в течение заданного времени (наработки) t при начале работы в нулевой момент времени:
Статистический показатель вероятности безотказной работы определяется как отношение числа объектов, безотказно проработавших до момента времени t, к числу объектов, исправных в начальный момент времени
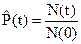 . (2)
. (2)
2. Вероятность отказа объекта на интервале времени от 0 до t
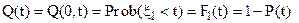 . (3)
. (3)
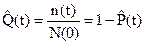 (4)
(4)
3. Вероятность безотказной работы объекта на интервале времени от t до t0
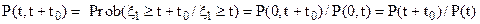 , (5)
, (5)
т.е. 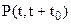 - есть условная вероятность того, что случайная наработка объекта до отказа окажется больше величины t+t0 при условии, что объект уже проработал безотказно до момента времени t.
- есть условная вероятность того, что случайная наработка объекта до отказа окажется больше величины t+t0 при условии, что объект уже проработал безотказно до момента времени t.
При статистической интерпретации это есть отношение числа объектов, проработавших до момента времени t+t0, к числу объектов, исправных к моменту t
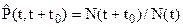 (6)
(6)
4. Плотность распределения отказов
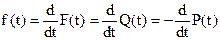 (7)
(7)
Статистическая плотность определяется как отношение числа отказов в интервале (t,t+Dt) к произведению числа исправных объектов в начальный момент времени t=0 на длительность интервала Dt
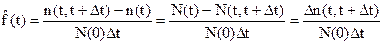 (8)
(8)
5. Интенсивность отказов объекта в момент времени t
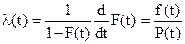 (9)
(9)
λ(t) – условная плотность вероятности отказа объекта к моменту времени t при условии, что до этого момента времени отказа объекта не было.
Статистическое определение показателя
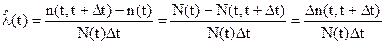 (10)
(10)
На рис.1. показана так называемая “ваннообразная” кривая, иллюстрирующая поведение интенсивности отказов на всех основных периодах жизни технических объектов. Период приработки, на котором выявляются и устраняются ошибки проектирования и производственные недостатки, имеет убывающую λ(t). Для моделирования этого этапа следует применять функции распределения с убывающей условной плотностью, например, распределение Вейбулла с параметром формы < 1. Период нормальной эксплуатации, при котором отказы вызываются случайными факторами и имеют постоянную интенсивность, адекватно описывается экспоненциальным распределением. В период старения, обусловленный износом оборудования, наблюдается возрастание λ(t). Здесь применяют “стареющие” распределения с возрастающей функцией интенсивности, например, распределение Вейбулла с параметром формы > 1.
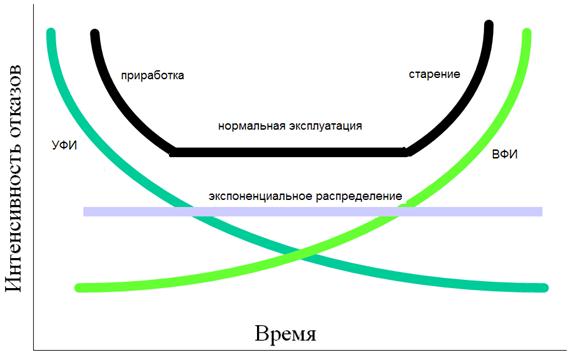
Рис. 1. “Ваннообразная” кривая (ВФИ – возрастающая функция интенсивности, УФИ – убывающая функции интенсивности)
6. Средняя наработка объекта до первого отказа (математическое ожидание случайной наработки до первого отказа)
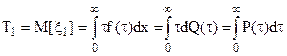 (11)
(11)
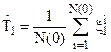 (12)
(12)
7. Гамма- процентная наработка до отказа Tg
Иногда бывает важно узнать значение наработки до отказа объекта, которая гарантируется с заданной вероятностью g. Очевидно, что величина Tg определяется как корень уравнения P(t)= g.
Используя формулу (9) можно записать 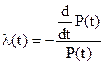 . Это соотношение позволяет выразить вероятность безотказной работы через интенсивность отказов. Для этого поменяем левую и правую части местами и возьмем от них интеграл в пределах от нуля до t:
. Это соотношение позволяет выразить вероятность безотказной работы через интенсивность отказов. Для этого поменяем левую и правую части местами и возьмем от них интеграл в пределах от нуля до t: 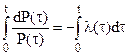 . Отсюда получаем
. Отсюда получаем 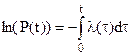 и далее
и далее
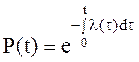 (13)
(13)
Полученное выражение (13) справедливо для любых распределений случайного времени работы до отказа. Иногда это соотношение называют “основным законом надежности”. Для экспоненциального распределения (13) преобразуется к виду
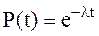 (14)
(14)
На основании (13), выражение для средней наработки до отказа (11) можно записать в виде
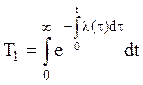 (15)
(15)
Для экспоненциального распределения имеем
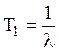 (16)
(16)
Показатели (1¸12) характеризуют случайное время появления первого отказа, поэтому они получили название – показатели безотказности. Показатели безотказности могут быть выражены один через другой, что продемонстрировано таблицей 1.
Таблица 1. Связь показателей безотказности
| P(t) | q(t) | f(t) | l(t) | |
| P(t) | P(t) | 1-q(t) | 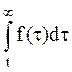 | 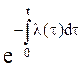 |
| q(t) | 1-P(t) | q(t) | 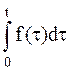 | 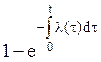 |
| f(t) | 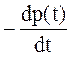 | 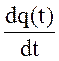 | f(t) | 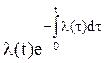 |
| l(t) | 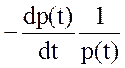 | 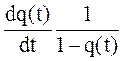 | 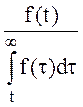 | l(t) |
II. Показатели надежности невосстанавливаемых объектов
Все приведенные выше показатели безотказности могут быть применены и для исследования надежности восстанавливаемых объектов. Однако, так как функционирование восстанавливаемых объектов имеет свои особенности, то для характеристики этих особенностей вводятся специальные показатели.
1. Средняя наработка между отказами T.
Процесс функционирования восстанавливаемого объекта представляет собой последовательность чередующихся случайных интервалов работы (ξk) и простоя (qk) (рис.2.). Простои наступают после отказа объекта, когда над ним проводятся восстановительные операции. Восстановление работоспособности может быть как полным (замена на аналогичный новый объект), так и частичным (например, ремонт только неисправной части).

Рис. 2. Стационарный участок функционирования восстанавливаемого объекта
В общем случае, при неполном восстановлении случайные времена ξk работы после k-1-го восстановления и до k-го отказа имеют разное распределение с плотностями fk(t). В этом случае средняя наработка между отказами T вычисляется как
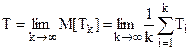 , (17)
, (17)
где каждая из средних наработок объекта от момента окончания k-1-го восстановления до k-го отказа определяется как
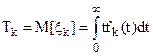 (18)
(18)
Или статистически
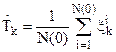 (19)
(19)
Если мы будем описывать процесс функционирования восстанавливаемого объекта с полным восстановлением его работоспособности, то в этом случае величины ξk и qk взаимно независимы и их распределение не зависит от k. В этом случае вычисления показателя средней наработки между отказами (17, 18) упрощаются, а процесс {ξ,q} носит название альтернирующего процесса.
2. Среднее время восстановления tв или математическое ожидание случайного времени восстановления q:
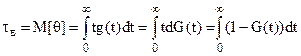 . (20)
. (20)
Здесь G(t) – функция распределения случайного времени восстановления, g(t) – плотность распределения времени восстановления
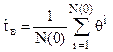 . (21)
. (21)
3. Интенсивность восстановления объекта
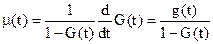 (22)
(22)
m(t) – условная плотность восстановления объекта в момент времени t при условии, что до этого момента времени восстановление объекта не произошло.
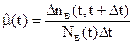 , (23)
, (23)
т.е. 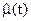 определяется как отношение числа восстановленных объектов в интервале (t,t+Dt) (Dnв(t,t+Dt)) к произведению числа еще не восстановленных объектов к моменту времени t (Nв(t)) на длительность интервала Dt.
определяется как отношение числа восстановленных объектов в интервале (t,t+Dt) (Dnв(t,t+Dt)) к произведению числа еще не восстановленных объектов к моменту времени t (Nв(t)) на длительность интервала Dt.
4. Важной количественной характеристикой потока отказов восстанавливаемого объекта в момент времени t является показатель - параметр потока отказов w(t). Этот показатель определяется как производная по времени от среднего числа отказов на интервале (0,t) – Nср(t):
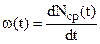 . (24)
. (24)
Статистическое определение
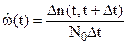 , (25)
, (25)
где N0 – количество восстановленных объектов в момент времени t.
Выражение (24) не является расчетной формулой. Вопрос аналитического определения показателя w(t) будет рассмотрен при изучении марковских моделей анализа надежности.
Существует ряд комплексных показателей надежности восстанавливаемых объектов, совместно характеризующих их свойства безотказности и ремонтопригодности. Важнейшими из них являются показатели готовности и оперативной готовности.
6. Коэффициент готовности Kг(t).
Kг(t) – есть вероятность застать объект в работоспособном состоянии в произвольный момент времени t. На практике обычно используется асимптотическое значение показателя, обозначаемое как Kг и называемое стационарным коэффициентом готовности:
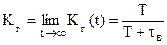 , (26)
, (26)
т.е. стационарный коэффициент готовности определяется как отношение средней наработки между отказами к сумме средней наработки между отказами и среднего времени восстановления.
Вопрос аналитического определения нестационарного коэффициента готовности будет подробно рассмотрен при изучении марковских и логико-вероятностных моделей надежности.
Статистическое определение показателя
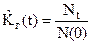 , (27)
, (27)
где Nt – число объектов работоспособных в момент времени t.
7. Коэффициент оперативной готовности Kог(t,t0).
Kог(t,t0) – вероятность того, что объект окажется работоспособным в произвольный момент времени t и далее проработает безотказно в течение интервала времени (t,t0).
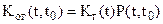 . (28)
. (28)
Статистическое определение
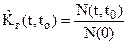 , (29)
, (29)
где N(t,t0) – число объектов исправных в момент t и безотказно проработавших в интервале (t,t0).
8. Коэффициент технического использования Kи
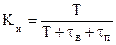 (30)
(30)
Показатель аналогичен стационарному коэффициенту готовности, но учитывает не только время ремонта, но и простои объекта, связанные с техническими осмотрами и профилактическим обслуживанием tп.
При проведении анализа надежности необходимо помнить, что коэффициент готовности является “точечным” показателем, определяющим надежность объекта в заданный момент времени, в отличии от вероятности безотказной работы, характеризующей надежность на интервале. Для демонстрации этого факта на рис.3. приведена временная эпюра работы 10 устройств, поставленных на испытание. Показатели коэффициент готовности и вероятность безотказной работы определяются каждый час в течение 10 часов.
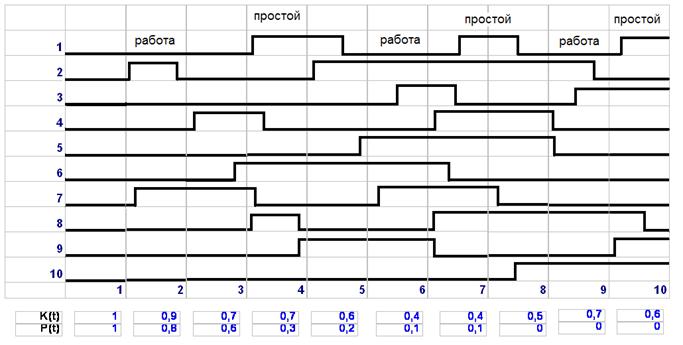
Рис.3. Статистическое определение коэффициента готовности и вероятности безотказной работы.
Литература к лекции 3.
- Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности. – М.: Наука, 1965.
- Надежность технических систем: Справочник / Ю.К. Беляев, В.А.Богатырев, В.В. Болотин и др.; под ред. И.А.Ушакова. М.: Радио и связь, 1985
- Кондратенков В А., Котельников Г.Н., Мамченков В.Л., Отрохов В.П. Вопросы теории надежности техничских систем. Смоленск.: Русич, 1998.
- Азарсков В.Н., Стрельников В.П. Надежность систем управления и автоматики. К.: НАУ, 2004.
 2014-02-09
2014-02-09 6316
6316
