Теорема умножения вероятностей

Вероятность произведения двух событий равна вер-ти одного из них, умноженной на условную вероятность другого при наличии первого:

Р (АВ) = Р(А) · Р(В/А), или Р (АВ) = Р(В) · Р(А/В).

Следствие. Вероятность совместного наступления двух независимых событий А и В равна произведению вероятностей этих событий:

Р (АВ) = Р(А) · Р(В).

Следствие. При производимых n одинаковых независимых испытаниях, в каждом из которых события А появляется с вероятностью р, вероятность появления события А хотя бы один раз равна 1 - (1 - р)^n.

Задание. В урне 2 белых и 3 черных шара. Из урны вынимают подряд два шара и назад не возвращаются. Найти вероятность того, что оба шара белые.

Решение. Пусть событие 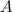- появление двух белых шаров. Это событие представляет собой произведение двух событий:

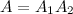
где событие 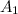- появление белого шара при первом вынимании, 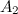- появление белого шара при втором вынимании. Тогда по теореме умножения вероятностей

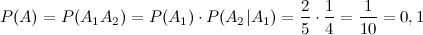
Ответ.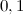

9. Вероятность суммы совместных событи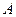й и 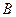равна:

.

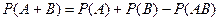Здесь слова «вероятность совместных событий» имеют принципиальное значение, т.к. для несовместных событий получается несколько иная теорема. Разберёмся в этом. Для несовместных событи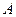й и 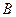основным свойством является равенство (они вместе произойти не могут):

.

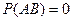Поэтому теорема переписывается в следующем виде.

Теорема о сложении вероятностей несовместных событий. Вероятность суммы несовместных событи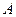й и 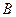равна:

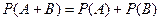. Пример. «Не кладите все яйца в одну корзину». В два банка положены деньги (слава Богу, что некто догадался положить их именно в два банка). Банки работают независимо друг от друга (часто встречающаяся ситуация). Вероятность разорения первого банка равна 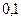, а второго - 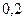. Какова вероятность того, что деньги сохранятся хотя бы в одном из банков.

Решение. Чтобы решить вероятностную задачу, главное, ввести правильные обозначения. Попробуем ввести следующие события.

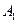- деньги взяты из первого банка,

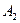- деньги взяты из второго банка.

Тогда событие 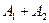означает, что деньги взяты либо из первого, либо из второго банка, либо из обоих банков сразу (вам очень повезло). А найти нужно именно вероятность этого события 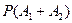. По формуле сложения вероятностей совместных событий получаем:

.

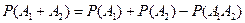Вероятность 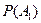того, что первый банк останется «на плаву», составляет с вероятностью 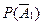того, что первый банк разорится, в сумме 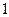(т.к. событие 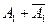есть достоверное событие). Поэтому:

.

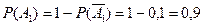Аналогично найдем

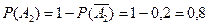.А вероятность произведения двух событий 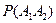равна произведению вероятностей 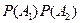, как произведение независимых событий. Поэтому:

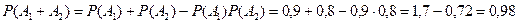.То есть искомая вероятность получается больше вероятносте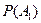й и 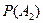, а, значит, права пословица!

10. Предположим, что событие 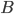может осуществляться только с одним из несовместных событий 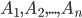. Например, в магазин поступает одна и та же продукция от трех предприятий в разном количестве. Существует разная вероятность выпуска некачественной продукции на разных предприятиях. Случайным образом отбирается одно из изделий. Требуется определить вероятность того, что это изделие некачественное (событие 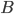). Здесь события 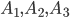— это выбор изделия из продукции соответствующего предприятия.

В этом случае вероятность события 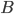можно рассматривать как сумму произведений событий

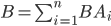
По теореме сложения вероятностей несовместных событий получаем

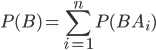
Используя теорему умножения вероятностей, находим

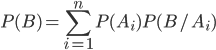(3.1)

Формула (3.1) носит название формулы полной вероятности.

Пример. Для рассмотренного выше случая с поступлением товара в магазин от трех предприятий зададим численные значения. Пусть от первого предприятия поступило 20 изделий, от второго — 10 изделий и от третьего — 70 изделий. Вероятности некачественного изготовления изделия на предприятиях соответственно равны 0,02; 0,03 и 0,05.

Определить вероятность взятия некачественного изделия.

Решение. Вероятности событий 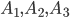будут равны P(А₁) = 0,2; P(А₂) = 0,1; P(А₃) = 0,7. Используя формулу (3.1), находим

P(B) = 0,2×0,02 + 0,1×0,03 + 0,7×0,05 = 0,042.

1.

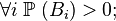
2.

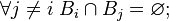
3. Пусть 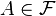— интересующее нас событие. Тогда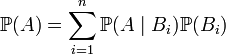

11.

Пусть событие 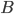происходит одновременно с одним из 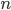несовместных событий 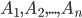. Требуется найти вероятность события 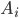, если известно, что событие 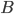произошло.

На основании теоремы о вероятности произведения двух событий можно написать

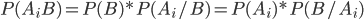
Откуда

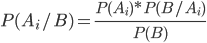
или

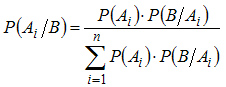(3.2)

Формула (3.2) носит название формулы Байеса.

Пример. Три организации представили в контрольное управление счета для выборочной проверки. Первая организация представила 15 счетов, вторая — 10, третья — 25. Вероятности правильного оформления счетов у этих организаций известны и соответственно равны: 0,9; 0,8; 0,85. Был выбран один счет и он оказался правильным. Определить вероятность того, что этот счет принадлежит второй организации.

Решение. Пусть 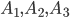— события выбора счета у первой, второй и третьей организаций. Соответствующие вероятности будут

, ,

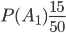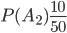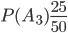
По формуле полной вероятности определяем вероятность выбора правильно оформленного счета

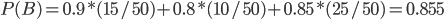
По формуле Байеса находим исходную вероятность

.

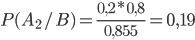12. Ряд классических распределений связан с экспериментом, в котором проводятся последовательные независимые испытания и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.

Последовательные испытания называются независимыми, если вероятность осуществления любого исхода в n-м по счету испытании не зависит от реализации исходов предыдущих испытаний.
Простейшим классом повторных независимых испытаний является последовательность независимых испытаний с двумя исходами («успех» и «неуспех») и с неизменными вероятностями «успеха» (р) и «неуспеха» (1 - p = q) в каждом испытании (схема испытаний Бернулли).

Вероятность получить ровно m успехов в n независимых испытаниях вычисляется по формуле, называемой формулой Бернулли.

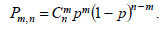
Определение. Число наступлений события А называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события А любое другое количество раз. Наивероятнейшее число наступлений события А в n испытаниях заключено между числами

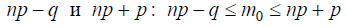
Если np - q — целое число, то наивероятнейших чисел два np - q и np + p.

14. Определение

Пусть задано вероятностное пространство 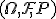. Случайной величиной, заданной на этом пространстве, называется числовая функция 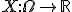, которая ставит в соответствие каждому элементарному исходу 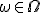число 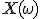- значение случайной величины на этом исходе. Данная функция должна быть 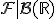-измеримой (где 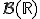- борелевская сигма-алгебра на прямой), т.е. для любого борелевского множества 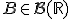его полный прообраз при отображении 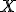должен быть событием: .

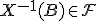Свойства

Случайная величина может быть интерпретирована как некоторое измерение, в результате которого при каждой реализации случайного опыта мы получаем некоторое число.

Случайная величина 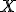индуцирует (порождает) новое вероятностное пространство 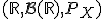с мерой 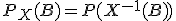, которая называется распределением вероятностей 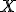. При исследовании одной только случайной величины иногда сразу задают это пространство и не вводят саму величину как отображение (хотя это всегда можно сделать, взяв тождественное отображение числовой прямой на себя). Вероятность 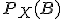также обозначают .

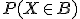Универсальный способ задания распределения случайной величины - через функцию распределения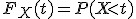

Наиболее часто используемые типы случайных величин

В практических приложениях наиболее часто используются два типа случайных величин: дискретные и абсолютно непрерывные, хотя, разумеется, существуют случайные величины, не относящиеся ни к одному из этих классов.