1. 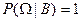 ;
;
2. 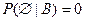 ;
;
3. 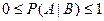 ;
;
4. если 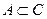 , то
, то 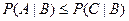 ;
;
5. 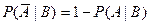 .
.
Формулу (3.1) можно переписать в виде
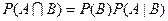 . .
| (3.2) |
Равенство (3.2) называют теоремой умножения для двух событий. С помощью (3.2) по индукции легко доказывается более общая
Теорема 3.1 (Теорема умножения). Пусть события 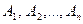 таковы, что
таковы, что 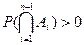 , тогда
, тогда
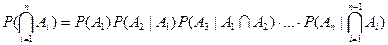 . .
| (3.3) |
Пример 3.1. В читальном зале имеется шесть учебников по теории вероятностей, из которых три в переплете. Библиотекарь взял два учебника. Найти вероятность того, что оба учебника в переплете.
Решение. Введем обозначения: событие 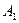 – первый взятый учебник имеет переплет,
– первый взятый учебник имеет переплет, 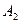 – второй учебник имеет переплет. Вероятность того, что оба учебника имеют переплет, вычисляется по формуле (3.2):
– второй учебник имеет переплет. Вероятность того, что оба учебника имеют переплет, вычисляется по формуле (3.2):
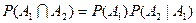 .
.
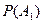 – вероятность того, что первый учебник имеет переплет,
– вероятность того, что первый учебник имеет переплет, 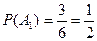 .
. 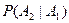 – вероятность того, что второй учебник имеет переплет, при условии, что первый взятый учебник был в переплете,
– вероятность того, что второй учебник имеет переплет, при условии, что первый взятый учебник был в переплете, 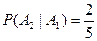 , следовательно
, следовательно
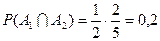 .
.
 2015-06-10
2015-06-10 496
496








