1. Если события 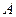 и
и 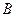 – независимые, то независимыми так же являются следующие пары событий:
– независимые, то независимыми так же являются следующие пары событий: 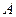 и
и 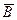 ,
, 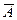 и
и 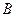 ,
, 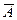 и
и 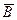 .
.
2. Пусть событие 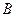 таково, что
таково, что 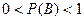 . События
. События 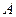 и
и 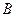 – независимы тогда и только тогда, когда выполнено соотношение:
– независимы тогда и только тогда, когда выполнено соотношение:
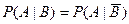 .
.
3. Если событие 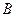 таково, что
таково, что 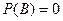 или
или 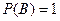 , то любое событие
, то любое событие 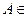 A не зависит от
A не зависит от 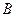 .
.
Определение 3.3. События 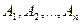 называются независимыми в совокупности, если для любых
называются независимыми в совокупности, если для любых 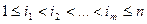 ,
, 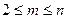 , выполняются равенства
, выполняются равенства
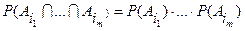 , , |
в противном случае события называются зависимыми.
Если в теореме 3.1. события 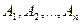 являются независимыми в совокупности, то формула (3.3) примет вид
являются независимыми в совокупности, то формула (3.3) примет вид
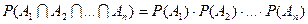 . . | (3.5) |
То есть вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий.
Пример 3.2. Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания первого стрелка равна 0,8, а второго – 0,6. Найти вероятность того, что 1) оба стрелка попали по мишени; 2) только первый стрелок попал по мишени.
Решение. Введем обозначения: событие 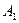 – первый стрелок попал в мишень,
– первый стрелок попал в мишень, 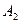 – второй стрелок попал в мишень. По условию:
– второй стрелок попал в мишень. По условию: 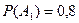 ,
, 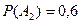 .
.
1) Событие 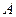 – оба стрелка попали по мишени. Данное событие наступит при одновременном попадании стрелков, поэтому
– оба стрелка попали по мишени. Данное событие наступит при одновременном попадании стрелков, поэтому 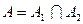 . В силу независимости событий
. В силу независимости событий 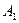 и
и 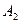 имеем:
имеем: 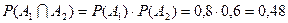 .
.
2) Событие 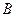 – только первый стрелок попал по мишени. Данное событие наступит тогда, когда первый стрелок попадет, а второй не попадет по мишени, поэтому
– только первый стрелок попал по мишени. Данное событие наступит тогда, когда первый стрелок попадет, а второй не попадет по мишени, поэтому 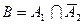 .
. 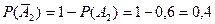 . В силу свойств независимых событий, события
. В силу свойств независимых событий, события 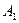 и
и 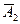 так же являются независимыми, откуда получаем
так же являются независимыми, откуда получаем 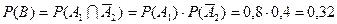 .
.
 2015-06-10
2015-06-10 1010
1010








