Определение 2.15. Относительной частотой события называют отношение числа испытаний, в которых событие произошло, к общему числу фактически произведенных испытаний.
Таким образом, относительная частота события А определяется формулой:
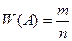 ,
,
где 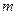 – число появлений события,
– число появлений события, 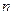 – общее число испытаний.
– общее число испытаний.
Сравнивая классическое определение вероятности и определение относительной частоты, можно сделать вывод, что определение вероятности не требует, чтобы испытания проводились в действительности (то есть вычисляется до опыта), а определение относительной частоты предполагает, что испытания были проведены фактически (то есть вычисляется после опыта).
Длительные наблюдения показали, что если в одинаковых условиях производятся опыты, в каждом из которых число испытаний 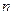 достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.
достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.
Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.
Пример 2.16. Многократно проводились опыты бросания монеты, в которых подсчитывали число появления герба. Результаты нескольких опытов приведены в таблице 2.1.
Таблица 2.1
| Число бросаний | Число появлений герба | Относительная частота |
| 4040 | 2048 | 0,5069 |
| 12000 | 6019 | 0,5016 |
| 24000 | 12012 | 0,5005 |
Здесь относительные частоты незначительно отклоняются от числа 0,5, причем данное отклонение тем меньше, чем больше число испытаний (при 4040 испытаниях отклонение составляет 0,0069, а при 24000 – лишь 0,0005). Учитывая, что вероятность появления герба при подбрасывании монеты равна 0,5, видим, что относительная частота колеблется около вероятности.
 2015-06-10
2015-06-10 724
724








