При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра событий A это набор подмножеств пространства элементарных исходов 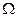 для которого выполняются следующие условия:
для которого выполняются следующие условия:
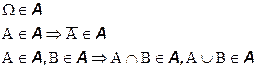
Сигма - алгебра событий F это набор подмножеств пространства элементарных исходов 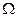 для которого выполняются следующие условия:
для которого выполняются следующие условия:
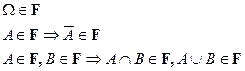
и для любой счетной последовательности

Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
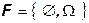
Если алгебра или сигма-алгебра содержит событие A, то она обязана содержать и отрицание A. Поэтому минимальное число подмножеств в нетривиальной сигма-алгебре равно 4.
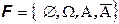
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
 2015-06-10
2015-06-10 7138
7138








