Различие между независимостью попарно и в совокупности. Пример Бернштейна

Данный пример показывает, что существуют попарно независимые события, которые не являются независимыми в совокупности.

Рассмотрим тетраэдр, грани которого покрашены в три цвета следующим образом:

1 грань – синяя

2 грань – зеленая

3 грань – желтая

4 грань разделена на три сектора – синий, зеленый и желтый.

Опыт состоит в бросании тетраэдра и наблюдении цвета выпавшей (нижней) грани.

Обозначим события

A – на грани есть синий цвет

B – на грани есть зеленый цвет

C – на грани есть желтый цвет

Тогда, используя симетричность тетраэдра и классическую вероятностную модель получим:

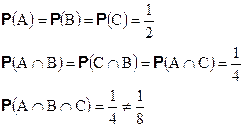
Для исключения неоднозначности при интерпретации понятия независимости в теории вероятностей при построении моделей используется, в основном, независимость в совокупности, как более сильная. В дальнейшем говоря о независимости мы, если не указано противное, будем подразумевать независимость в совокупности.