Множество положительности непрерывной функции

Пусть

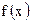
непрерывная функция. Тогда множество

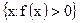
является борелевским.

Действительно, для любой точки x, в которой непрерывная функция положительна, найдется интервал, окружающий точку x, в котором эта функция также положительна. Для доказательства достаточно представить множество

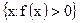
в виде объединения всех таких интервалов с рациональными центрами.

Другие множества

Пусть

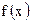
непрерывная функция.

Тогда множества

, , ,….

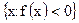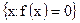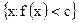являются борелевскими.