Неборелевские множества

Таким образом, можно привести массу примеров практически важных борелевских множеств. Возникает вопрос: может быть все множества на прямой борелевские?

Обозначим

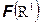
наибольшую сигма-алгебру, т.е. сигма-алгебру, включающую в себя все подмножества действительных чисел

Тогда, очевидно, что

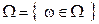
Но, оказывается, что

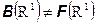
Доказательство этого утверждения (пример неборелевского множества на действительной прямой) содержится в курсе функционального анализа.

Варианты определения борелевской сигма-алгебры

Борелевская сигма-алгебра определена как минимальная сигма-алгебра, содержащая все интервалы вида

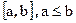
т.е.

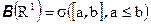
Ясно, теперь, что

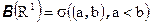
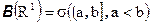
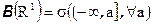
и т.д.