Доказательство завершено. Пусть теперь 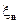и - две последовательности простых функций сходящиеся к

Пусть теперь и 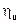- две последовательности простых функций сходящиеся к 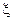. Тогда дважды используя лемму, получаем, что одновременно должны выполняться два неравенства

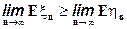
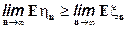
что доказывает равенство

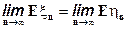
т.е. определение корректно.

Для произвольной случайной величины положим

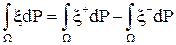
если хотя бы один из этих интегралов конечен.

Скажем, что у случайной величины

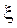
конечное математическое ожидание, если конечны оба этих интеграла, или что то же самое, конечен интеграл

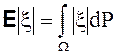
Свойства интегралов от простых случайных величин переносятся на случай произвольных случайных величин без изменений. Доказательства этих свойств состоят, по существу, из доказательств обоснованности предельного перехода в соответствующих формулах. Для этого используются следующие теоремы о предельном переходе под знаком интеграла Лебега, доказательства которых содержатся в курсе функционального анализа.

Заметим, что свойство нормированности вероятности 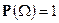при построении интеграла не использовалось. Таким образом можно строить интегралы по произвольным мерам.