Пусть 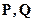 - две сигма-конечные меры и
- две сигма-конечные меры и 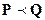 . Тогда существует и единственна с точностью до значений на множестве
. Тогда существует и единственна с точностью до значений на множестве 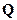 меры нуль функция
меры нуль функция 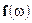 такая, что
такая, что
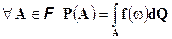
Единнственность с точностью до значений на множестве 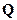 меры нуль означает, что если
меры нуль означает, что если 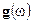 - другая функция, удовлетворяющая условию
- другая функция, удовлетворяющая условию
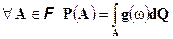 , то
, то
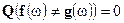
Случайная величина 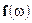 называется производной Радона-Никодима меры
называется производной Радона-Никодима меры 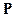 относительно меры
относительно меры 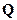 или плотностью меры
или плотностью меры 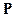 относительно меры
относительно меры 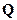 и обозначается так
и обозначается так
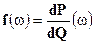
Если мера 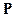 абсолютно непрерывна относительно меры
абсолютно непрерывна относительно меры 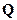 , то можно заменять вычисление интеграла Лебега по мере
, то можно заменять вычисление интеграла Лебега по мере 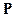 на вычисление интеграла Лебега по мере
на вычисление интеграла Лебега по мере 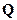 , что показывает следующая лемма
, что показывает следующая лемма
Лемма.
Пусть 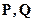 - две сигма-конечные меры и
- две сигма-конечные меры и 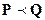 . Тогда для любой случайной величины
. Тогда для любой случайной величины 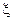
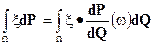
 2015-06-10
2015-06-10 316
316








