2015-06-10
464
Вычислим математическое ожидание и дисперсию для наиболее важных распределений.
| Название распределения | Математическое ожидание | Дисперсия |
| Вырожденное в точке a | a | |
| Биномиальное (n,p) |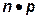 
| 
|
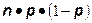
| Геометрическое p |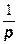 
| 
|
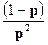
Пуассоновское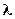 
|
|
|
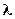
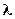
| Нормальное стандартное | ||
Нормальное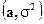 
| 
| 
|
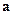
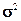
| Равномерное на отрезке (0,1) | 1/2 | 1/12 |
| Равномерное на отрезке (A,B) |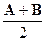 
| 
|
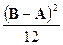
Бета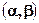 
| 
| 
|
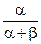
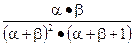
| Экспоненциальное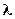
| 
| 
|
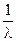
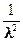
Гамма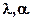 
| 
| 
|
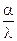
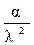
Если случайные величины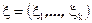 
имеют многомерное нормальное распределение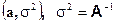 
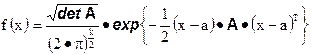
то
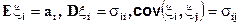
Вычисление всех характеристик представляет собой, по существу, упражнения из математического анализа по суммированию рядов и взятию интегралов. Упростить в ряде случаев эти вычисления можно, если представить исследуемую случайную величину в виде суммы независимых случайных величин и воспользоваться свойствами математического ожидания и дисперсии.
