2015-06-10
690
Следующая теорема показывает, что из поточечной сходимости плотностей следует сходимость соответствующих им мер по вариации
Теорема Шеффе
Пусть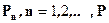 
- вероятностные меры, абсолютно непрерывные относительно меры 
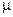и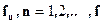 
- соответствующие плотности мер 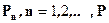относительно меры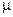
Тогда, если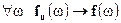 
, то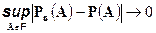 
Доказательство этой теоремы проведите самостоятельно по схеме доказательства соответствующего утверждения в теореме Пуассона с использованием теоремы Лебега о мажорированной сходимости.
