Теорема единственности для характеристических функций и характеристические функции важных распределений

Соответствие между функциями распределения и характеристическими функциями является взаимнооднозначным. Каждой функции распределения соответствует одна и только одна характеристическая функция. Это свойство позволяет использовать характеристические функции для различения и определения распределений случайных величин. Прежде чем доказывать теорему единственности, подсчитаем характеристические функции наиболее важных распределений.

Название распределения	Характеристическая функция
Вырожденное в точке a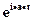
Биномиальное (n,p)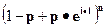
Геометрическое p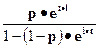
Пуассоновское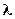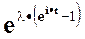
Нормальное стандартное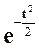
Нормальное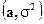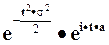
Равномерное на отрезке (0,1)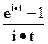
Равномерное на отрезке (a,b)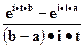
Бета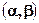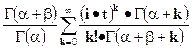
Экспоненциальное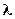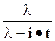
Гамма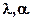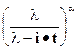

Заметим, что плотность и характеристическая функция стандартной нормальной случайной величины отличаются лишь множителем. Это позволяет нам доказать следующее важное равенство.