2015-06-10
245
Очевидные свойства характеристической функции приведем без доказательства
1. Характеристическая функция существует для любой случайной величины
2. 
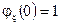
3. 
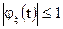
4. 
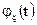равномерно непрерывна. Действительно
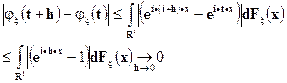
по теореме Лебега о мажорируемой сходимости.
5. Если существует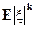 
для некоторого k=1,2,..., то существует и 
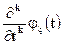причем
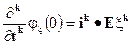. Для доказательства достаточно продифференцировать необходимое количество раз интеграл, определяющий характеристическую функцию, по параметру t.
6. 
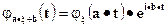
7. Пусть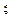 
и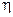 
- две независимые случайные величины, тогда
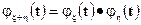. Это следует их того, что математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий.
8. Если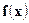 
- плотность случайной величины 
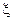, то
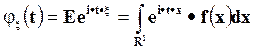- является преобразованием Фурье плотности. Подробно свойства преобразования Фурье рассматриваются в курсе математического анализа.
