2015-06-10
977
Пусть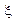 
- случайная величина с функцией распределения 
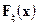и характеристической функцией 
,
.
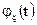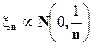Тогда плотность случайной величины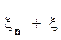 
можно представить в виде
.
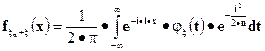Доказательство.
Пусть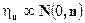 
Рассмотрим очевидное равенство
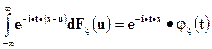
умножим его на плотность случайной величины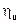 
и проинтегрируем по t от 
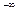до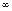 
.Учитывая, что
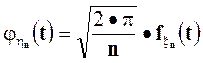
получим требуемое утверждение
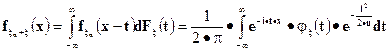
Доказательство завершено.
Меняя в доказательстве местами случайные величины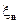 
и 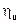получаем следующий вариант равенства Парсеваля
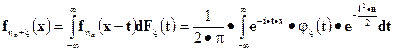
Очевидно, приведенные формулы справедливы и для несобственных функций распределения.
