Преобразование Лапласа и производящая функция

Если случайная величина неотрицательна, то для любого неотрицательного s всегда существует

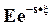
которое называется преобразование Лапласа распределения случайной величины .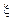

Если случайная величина неотрицательна и целочисленна, то для любого z такого, что 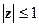всегда существует

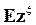
которое называется производящей функцией случайной величины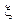

Заменой переменных эти преобразования можно выразить через характеристическую функцию.