2015-06-10
652
Говорят, что случайная величина 
имеет биномиальное распределение с параметрами 
и 
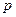, где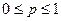 
, и пишут 
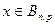, если принимает значения 0, 1, …, с вероятностями 
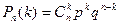. Случайная величина с таким распределением имеет смысл числа успехов в испытаниях схемы Бернулли с вероятностью успеха 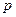. Таблица распределения имеет вид
| … | 
| … |
| ||
| 
| 
| … | 
| … | 
|
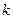
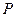
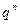
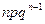
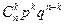
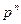
Таким образом, биномиальным называют распределение вероятностей, определяемое формулой Бернулли
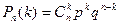. (1)
Закон назван биномиальным потому, что правую часть формулы Бернулли можно рассматривать как общий член разложения бинома Ньютона:
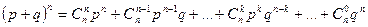
или, с учетом того, что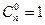 
, 
, 
,
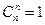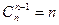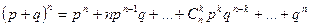
Таким образом, первый член разложения 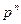определяет вероятность наступления рассматриваемого события раз в независимых испытаниях; второй член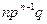 
определяет вероятность наступления события 
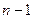раз; последний член 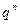определяет вероятность того, что событие не появится ни разу.
Например: Монета брошена 2 раза. Найти закон распределения случайной величины - числа выпадений «герба».
§ При каждом бросании монеты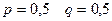 
. При двух бросаниях монеты «герб» может появиться 2, 1 раз или вообще не появиться. Таким образом, 
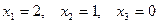. Соответствующие вероятности рассчитаем по формуле Бернулли:
; 
; 
.
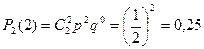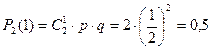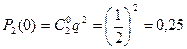Искомый закон распределения
|
| |||
|
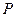
| 0,25 | 0,5 | 0,25 |
Контроль: 0,25+0,5+0,25=1. §
