Предположим, что необходимо вычислить вероятность не менее десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 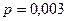 . Вероятность этого события равна любому из следующих выражений:
. Вероятность этого события равна любому из следующих выражений:
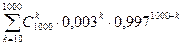 или
или 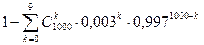 .
.
Но вычисление даже одного слагаемого в каждом из этих выражений весьма проблематично.
Сформулируем теорему о приближенном вычислении вероятности 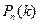 какого-либо числа успехов в большом числе
какого-либо числа успехов в большом числе  испытаний схемы Бернулли с маленькой вероятностью
испытаний схемы Бернулли с маленькой вероятностью 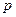 успеха.
успеха.
Т. Пусть 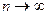 ,
, 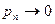 так, что
так, что 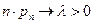 . Тогда для любого
. Тогда для любого 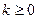 вероятность получить
вероятность получить 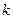 успехов в
успехов в  испытаниях схемы Бернулли с вероятностью успеха
испытаниях схемы Бернулли с вероятностью успеха 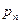 стремится к величине
стремится к величине 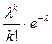 , т.е.
, т.е.
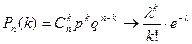 .
.
¨ Положим 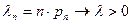 . По свойству 1,
. По свойству 1, 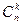 ~
~ 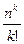 при фиксированном
при фиксированном 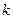 и при
и при 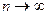 . Тогда
. Тогда
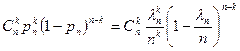 ~
~ 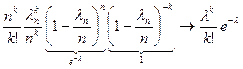 . (*)
. (*)
В (*) мы использовали свойство 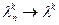 и второй замечательный предел.
и второй замечательный предел.
Для доказательства теоремы осталось в формуле (*) воспользоваться свойством 2. ¨
Таким образом, вероятность какого-либо числа успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью успеха приближенно равна:
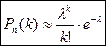 . (4)
. (4)
Формула (4) называется формулой Пуассона.
Замечание. Существуют специальные таблицы, пользуясь которыми можно найти значения 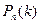 , зная
, зная 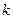 и
и 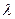 .
.
Формула Пуассона используется в задачах, относящихся к редким событиям (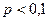 ,
, 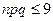 ).
).
Например: Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
§ По условию 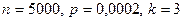 . Найдем
. Найдем 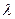 :
:
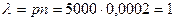 .
.
По формуле (4) искомая вероятность приближенно равна
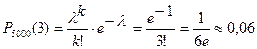 . §
. §
 2015-06-10
2015-06-10 1111
1111








