Пусть производится  независимых испытания, в каждом из которых вероятность появления события
независимых испытания, в каждом из которых вероятность появления события  постоянна и равна
постоянна и равна 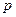 .
.
Т-ма 4. (Интегральная теорема Лапласа.)
Если вероятность 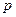 появления события
появления события  в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 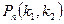 того, что событие
того, что событие  появится в
появится в  испытаниях от
испытаниях от 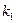 до
до 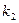 раз, приближенно равна определенному интегралу
раз, приближенно равна определенному интегралу
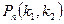
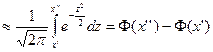 , (6)
, (6)
где 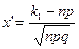 и
и 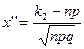 . Здесь
. Здесь 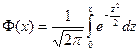 - функция Лапласа.
- функция Лапласа.
Значения интеграла 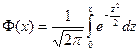 приведены в приложениях. В таблице даны значения функции
приведены в приложениях. В таблице даны значения функции 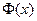 для положительных значений x и для
для положительных значений x и для 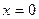 . Надо помнить, что
. Надо помнить, что 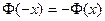 . При
. При 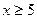 можно принять
можно принять 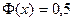 .
.
Пример 2.Вероятность брака среди деталей 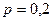 . Найти вероятность того, что среди 200 деталей число бракованных от 60 до 80.
. Найти вероятность того, что среди 200 деталей число бракованных от 60 до 80.
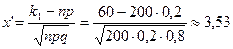 ,
, 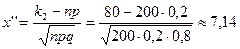 .
.
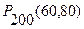
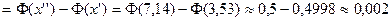 .
.
 2015-06-10
2015-06-10 460
460








