Пусть нулевая гипотеза 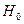 состоит в том, что выборка
состоит в том, что выборка 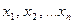 объема
объема  соответствует СВ
соответствует СВ  с ФР
с ФР 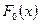 . Для статистической проверки этой гипотезы используем критерий
. Для статистической проверки этой гипотезы используем критерий 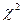 . Разобьем числовую ось на
. Разобьем числовую ось на 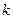 интервалов
интервалов 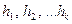 . Обозначим через
. Обозначим через 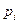 вероятность того, что значение СВ
вероятность того, что значение СВ  попадет в интервал
попадет в интервал 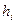 . Эти вероятности вычисляются по известной ФР
. Эти вероятности вычисляются по известной ФР 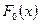 . Обозначим через
. Обозначим через 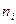 число элементов выборки, попавших в интервал
число элементов выборки, попавших в интервал 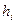 . За меру отклонения распределения выборки от гипотетического
. За меру отклонения распределения выборки от гипотетического 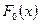 примем величину
примем величину
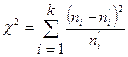 ,
,
где 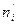 - теоретические частоты.
- теоретические частоты.
Пирсон доказал, что в случае справедливости гипотезы 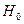 распределение СВ
распределение СВ 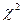 с при
с при 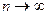 сходится к распределению
сходится к распределению 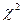 с
с 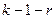 степенями свободы (
степенями свободы (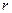 - число параметров предполагаемого распределения). Зададим уровень значимости
- число параметров предполагаемого распределения). Зададим уровень значимости 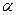 , т.е. вероятность столь малую, что событие с такой вероятностью будем считать практически невозможным при одном испытании. Обычно полагают
, т.е. вероятность столь малую, что событие с такой вероятностью будем считать практически невозможным при одном испытании. Обычно полагают 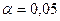 или
или 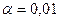 . Находим по таблице распределения
. Находим по таблице распределения 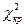 такое значение
такое значение 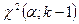 , что
, что 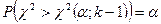 . Далее вычислим по имеющейся выборке
. Далее вычислим по имеющейся выборке 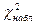 .
.
И если окажется, что 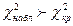 , то такое отклонение значимо, и мы с уровнем значимости
, то такое отклонение значимо, и мы с уровнем значимости 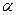 отвергаем гипотезу
отвергаем гипотезу 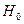 как не согласующуюся с опытными данными.
как не согласующуюся с опытными данными.
Если же получим 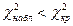 , то это значит, что данная выборка согласуется с гипотезой
, то это значит, что данная выборка согласуется с гипотезой 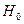 .
.
 2015-06-10
2015-06-10 331
331







