Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.
Для определения точности оценки используют доверительный интервал, а для определения надежности – доверительную вероятность.
Пусть для параметра 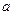 получена из опыта несмещенная оценка
получена из опыта несмещенная оценка 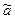 . Требуется оценить возможную при этом ошибку. Зададим некоторую вероятность
. Требуется оценить возможную при этом ошибку. Зададим некоторую вероятность 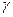 , например
, например 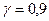 , и найдем такое значение
, и найдем такое значение 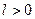 , для которого
, для которого
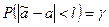 или
или 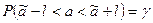 .
.
Т.е. неизвестное значение параметра попадет в интервал
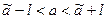 . (6)
. (6)
Опр. Доверительным называют интервал 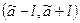 , который с заданной надежностью
, который с заданной надежностью 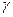 покрывает заданный параметр.
покрывает заданный параметр.
При этом надежностью или доверительной вероятностью называется вероятность того, что истинное значение параметра лежит в этом интервале.
Пусть произведено  независимых испытаний над СВ
независимых испытаний над СВ  с неизвестным МО
с неизвестным МО 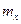 и дисперсией
и дисперсией 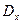 . На основании опытных данных для этих параметров получены оценки
. На основании опытных данных для этих параметров получены оценки
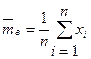 и
и 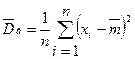 .
.
Доверительный интервал для МО приближенно равен
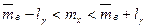 ,
,
где 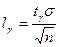 (без доказательства), где
(без доказательства), где 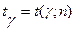 находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным  и
и 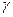 , а
, а 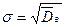 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Оценку
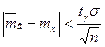 или
или 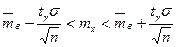 (7)
(7)
называют классической. Из формулы 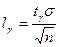 , определяющей точность классической оценки, делаем выводы:
, определяющей точность классической оценки, делаем выводы:
1. при увеличении  число
число 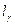 убывает, и следовательно, точность оценки увеличивается;
убывает, и следовательно, точность оценки увеличивается;
2. при увеличении надежности 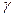 возрастает
возрастает 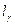 , и следовательно, точность оценки уменьшается.
, и следовательно, точность оценки уменьшается.
Пример 1. Произведено 20 опытов над величиной  . Результаты опытов приведены в таблице:
. Результаты опытов приведены в таблице:
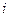 | ||||||||||
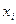 | 10,9 | 10,7 | 10,5 | 10,6 | 10,4 | 11,3 | 10,8 | 11,2 | 10,9 | |
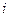 | ||||||||||
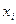 | 10,8 | 10,3 | 10,5 | 10,8 | 10,9 | 10,6 | 11,3 | 10,8 | 10,9 | 10,7 |
Найти интервальную оценку 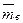 для МО (с надежностью
для МО (с надежностью 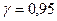 ) величины
) величины  .
.
►
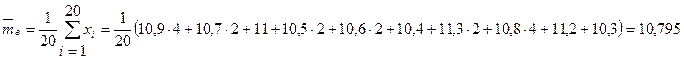 Так как
Так как 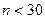 , используем исправленную дисперсию:
, используем исправленную дисперсию:
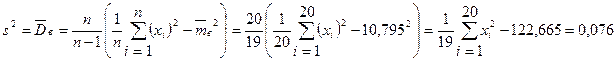 .
.
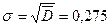 .
.
Найдем 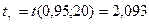 . По формуле (7):
. По формуле (7):
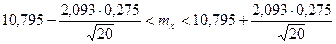 ,
, 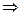
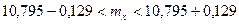
или 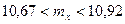 . ◄
. ◄
Интервальной оценкой (с надежностью 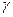 ) математического ожидания
) математического ожидания 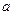 нормально распределенного количественного признака
нормально распределенного количественного признака  по выборочной средней
по выборочной средней 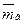 при неизвестном среднем квадратическом отклонении
при неизвестном среднем квадратическом отклонении 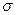 генеральной совокупности служит доверительный интервал:
генеральной совокупности служит доверительный интервал:
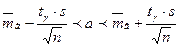 , (8)
, (8)
где 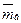 - выборочная средняя;
- выборочная средняя; 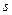 - «исправленное» выборочное среднее квадратическое отклонение;
- «исправленное» выборочное среднее квадратическое отклонение; 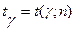 находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным  и
и 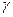 .
.
Интервальной оценкой (с надежностью 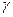 ) среднего квадратического отклонения
) среднего квадратического отклонения 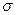 нормально распределенного количественного признака
нормально распределенного количественного признака  по «исправленному» выборочному среднему квадратическому отклонению
по «исправленному» выборочному среднему квадратическому отклонению 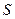 служит доверительный интервал:
служит доверительный интервал:
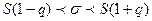 (при
(при 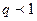 ), (9)
), (9)
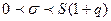 (при
(при 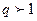 )
)
где 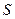 - «исправленное» выборочное среднее квадратическое отклонение;
- «исправленное» выборочное среднее квадратическое отклонение; 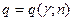 находим по таблице приложения 4 по заданным
находим по таблице приложения 4 по заданным  и
и 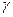 .
.
Пример 2. Произведено 10 независимых опытов над СВ  , распределенной нормально с неизвестными параметрами
, распределенной нормально с неизвестными параметрами 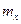 и
и 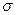 . Результаты опытов приведены в таблице:
. Результаты опытов приведены в таблице:
 | ||||||||||
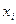 | 2,5 | -2,3 | 1,9 | -2,1 | 2,4 | 2,3 | -2,5 | 1,5 | -1,7 |
Найти оценку 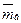 для МО и построить доверительный интервал (с надежностью
для МО и построить доверительный интервал (с надежностью 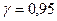 ).
).
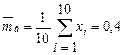 ,
, 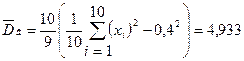 ,
, 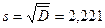 .
.
Найдем 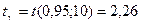 . Доверительный интервал:
. Доверительный интервал:
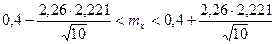 ,
, 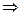
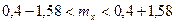
или 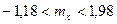 . ◄
. ◄
 2015-06-10
2015-06-10 1150
1150
