2015-06-10
716
Если n – велико, а р – отлично от 0 и 1, то вер-ть Pn(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна значению ф-ии:
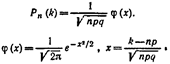
Значения ф-ии фи(х) для положительных х приведены в специальных таблицах. Для отрицательных значений аргумента исп. те же таблицы, т.к. ф-ия фи(х) четная. (фи от –х= фи от х)
Для того, чтобы посчитать вер-ть наступления не более чем m успехов, когда n велико, прим интегральную теорему Лапласа: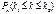 
= 
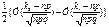
Замечание:ф-ия для Ф=2/2корня из пи...(в таблице). При Ф=1/2корня из пи.. 1/2 перед формулой убирается.
Осн. св-ва ф-ии Лапласа:
1.Ф(0)=0
2.Ф(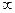
)=0,5
3.Ф(-t)=-Ф(t)
Для ф-ии Лапласа также есть таблицы ее значений. В таблице даются значения для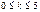 
. Для отр. знач. t исп св-во нечетности ф-ии, т.е. Ф(-t)=-Ф(t)
Если t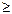 
5, то Ф(t)=0,5, для любого t 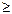5.
Теоремы Лапласа дают удовлетворительное приближение при np>=10. Чем ближе значения p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).
