Закон распределения ф-ции двух СВ

Задача опр. закона распр. ф-ции нескольких случ. аргументов значительно сложнее аналогичной задачи для ф-ции одного аргумента.

Имеется система двух непрерывных СВ (X, Y) с плотностью распр. f(x, y). Случ. вел-на Z связана с X и Y функциональной зависимостью: Z = φ(X, Y). Требуется найти закон распр. вел-ны Z. Ф-ция z = φ(x, y) изображается поверхностью, а не кривой, как в случае одного аргумента. Найдем ф-цию распр. вел-ны Z: G(z) = P(Z<z) = P(φ(X, Y)<z) – формула (1). Проведем плоскость Q, параллельную плоскости xOy, на расстоянии z от нее. Эта плоскость пересечет поверхность z = φ(x, y) по некот. кривой K. Спроектируем кривую К на плоскость xOy. Эта проекция, уравнение к-рой φ(x, y) = z, разделит плоскость xOy на две области; для одной из них высота поверхности над плоскостью xOy будет меньше, а для другой – больше z. Обозначим D ту область, для которой эта высота меньше z. Чтобы выполнялось нерав-во (1), случ. точка (X, Y), очевидно, должна попасть в область D; следовательно, G(z) = P((X,Y)ÌD)= 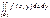- формула (2). В выражение (2) вел-на z входит неявно, через пределы интегрирования. Дифференцируя G(z) по z, получим плотность распр. вел-ны Z: g(z) = G'(z). Зная конкр. вид ф-ции z = φ(x, y), можно выразить пределы интегрирования через z и написать выражение g(z) в явном виде. Для того, чтобы найти закон распр. ф-ции двух аргументов, нет необходимости каждый раз строить поверхность z = φ(x, y) и пересекать ее плоскостью, параллельной xOy. На практике достаточно построить на плоскости xOy кривую, уравнение к-рой z = φ(x, y), отдать себе отчет, по какую сторону этой кривой Z<z, а по какую Z>z, и интегрировать по области D, для которой Z<z.