Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них постоянна и равна.
Пусть 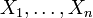 — конечная последовательность независимых случайных величин с распределением Бернулли, то есть
— конечная последовательность независимых случайных величин с распределением Бернулли, то есть
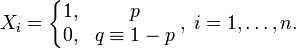
Построим случайную величину 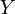 :
:
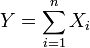 .
.
Тогда 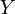 , число единиц (успехов) в последовательности
, число единиц (успехов) в последовательности 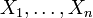 , имеет биномиальное распределение с
, имеет биномиальное распределение с 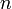 степенями свободы и вероятностью «успеха»
степенями свободы и вероятностью «успеха» 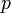 . Пишем:
. Пишем: 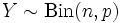 . Её функция вероятности задаётся формулой:
. Её функция вероятности задаётся формулой:
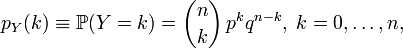
где 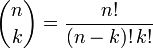 — биномиальный коэффициент.
— биномиальный коэффициент.
Функция распределения биномиального распределения может быть записана в виде суммы:
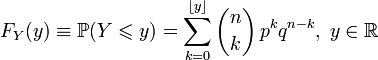 ,
,
где 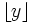 обозначает наибольшее целое, не превосходящее число
обозначает наибольшее целое, не превосходящее число 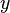 , или в виде неполной бета-функции:
, или в виде неполной бета-функции:
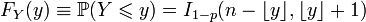 .
.
 2015-06-10
2015-06-10 540
540








