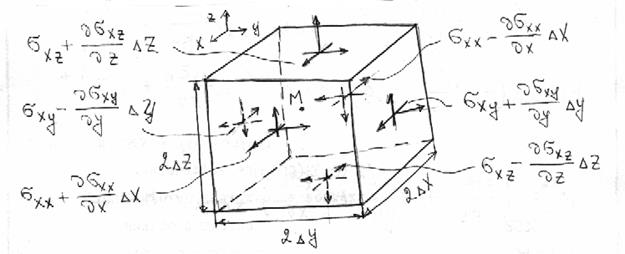
Рассмотрим окрестность точки М деформируемого тела, имеющего форму параллелепипеда с гранями, параллельными координатным плоскостям и центром в точке М. Длины ребер равны 2Dx, 2Dy, 2Dz.
Пусть sij – напряжения в точке М, действующие по плоскостям, проходящим через эту точку и параллельным граням параллелепипеда. На гранях параллелепипеда напряжения будут несколько отличаться от sij. На рисунке обозначены только те компоненты напряжений, действующих по граням, которые параллельны оси Х.
Определим составляющую SХ равнодействующей силы от напряжений на гранях элементарного параллелепипеда. Одинаковые напряжения на противоположных гранях отличаются на некоторое приращение.
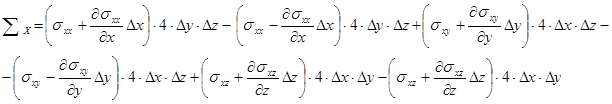 После преобразований
После преобразований
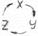
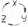 Если сила, действующая на единицу массы элементарного параллелепипеда
Если сила, действующая на единицу массы элементарного параллелепипеда 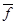 , скорость его движения
, скорость его движения 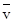 , а ускорение
, а ускорение 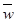 , то уравнения движения параллелепипеда запишутся так:
, то уравнения движения параллелепипеда запишутся так:
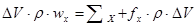
Здесь DV – объем параллелепипеда, r - плотность.
После преобразований получим
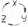
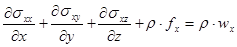 (1.14)
(1.14)
Уравнения (1.14) называются дифференциальными уравнениями движения. В тензорной форме они имеют вид
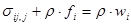 (1.15)
(1.15)
В частном случае, который чаще всего встречается в задачах теории ОМД, если отсутствуют массовые силы 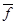 , а движение частиц достаточно медленное (r×wi » 0), уравнения (1.15) упрощаются
, а движение частиц достаточно медленное (r×wi » 0), уравнения (1.15) упрощаются
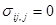 (1.16)
(1.16)
или в развернутом виде
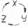
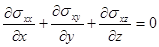 (1.17)
(1.17)
и называются уже дифференциальными уравнениями равновесия.
Дифференциальные уравнения движения (1.14) и даже дифференциальные уравнения равновесия (1.16) не образуют замкнутой системы уравнений, так как три уравнения (1.14) содержат при заданных массовых силах девять неизвестных (sij и v i), а в случае медленных течений в уравнения (1.17) входит шесть искомых компонентов тензора напряжения.
Примечание.
Наличие запятой в подстрочных индексах соотношений (1.15) и (1.16) означает дифференцирование по соответствующей координате (индексу).
 2015-06-10
2015-06-10 425
425







