2015-06-10
281
Решение вероятностных задач нередко требует использования случайных величин, которые представляют собой функции одного или нескольких аргументов – случайных величин. Простейшей среди них является функция одной СВ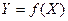 
. Как правило, закон распределения СВ Y неизвестен заранее. Его необходимо определить, исходя из особенностей случайного аргумента – СВ Х.
Пусть СВ Х дискретна и имеет ряд распределения:
| xi | x 1 | x 2 | … | xn |
| pi | p 1 | p 2 | … | pn |
Тогда СВ 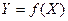соответствует ряд распределения:
| y |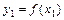 
| 
| … | 
|
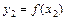
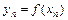
| pi | p 1 | p 2 | … | pn |
Пример.
Дискретная СВ Х задана законом распределения:
| xi | -2 | -1 | |||
| pi | 0,2 | 0,1 | 0,3 | 0,1 | 0,3 |
Найти закон распределения СВ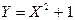 
.
Решение.
Найдем возможные значения :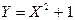
.
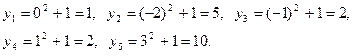Найдем их вероятности:
;
;
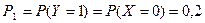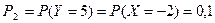Так как событие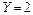 
есть сумма двух несовместных событи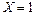й 
и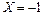 
, то по теореме о вероятности суммы несовместных событий:
;
.
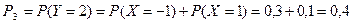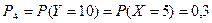Итак, ряд распределения СВ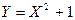 
имеет вид:
| yi | ||||
| pi | 0,2 | 0,1 | 0,4 | 0,3 |
