2015-06-10
266
Для упорядоченной пары случайных величин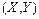 
функция 
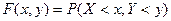называется функцией распределения случайного вектора .
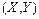Свойства функции распределения:
1. 
.
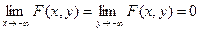2. 
, 
.
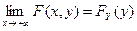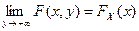3. 
.
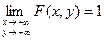4. 
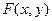- неубывающая функция своих аргументов.
5. 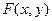непрерывна слева по каждому из своих аргументов.
Если компоненты вектора представляют собой ДСВ, то закон распределения случайного вектора можно задать перечислением всех возможных значений пар 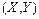и соответствующих им вероятностей 
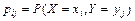, что удобно отображать в виде таблицы двумерного распределения вероятностей. Если компоненты вектора представляют собой НСВ, то закон распределения может быть задан при помощи функции двумерной плотности распределения вероятностей f (x, y), интегрирование которой дает функцию распределения:
.
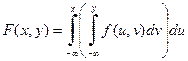Корреляционный момент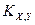 
случайных величин X и Y есть математическое ожидание
,
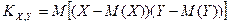то есть
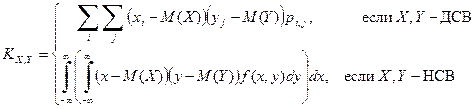
Случайные величины X и Y называются коррелированными, если их корреляционный момент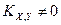 
.
Пример.
По заданному закону распределения случайного вектора определить законы распределения его компонент - СВ Х и СВ Y.
| Y\Х | |||
| 0,1 | 0,2 | 0,1 | |
| 0,3 | 0,1 | 0,2 |
Решение.
СВ Х принимает значения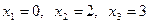 
. Событие 
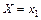есть сумма независимых между собой событи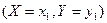й 
и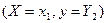 
. В результате вероятность этого события:
.
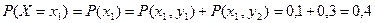Аналогично находим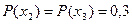 
. Таким образом, закон распределения СВ Х имеет ряд распределения:
| хi | |||
| pi | 0,4 | 0,3 | 0,3 |
Таким же образом находим закон распределения СВ Y:
| уi | ||
| pi | 0,4 | 0,6 |
